# 第 14 章_数据结构与集合源码

讲师：尚硅谷 - 宋红康（江湖人称：康师傅）

官网：http://www.atguigu.com

# 本章专题与脉络

主线：

常见的数据结构
集合中是如何使用数据结构实现的

第3阶段：Java高级应用-第14章

# 1. 数据结构剖析

我们举一个形象的例子来理解数据结构的作用：

** 战场：** 程序运行所需的软件、硬件环境
** 敌人：** 项目或模块的功能需求
** 指挥官：** 编写程序的程序员
** 士兵和装备：** 一行一行的代码
** 战术和策略：** 数据结构

上图：没有战术，打仗事倍功半

上图：有战术，打仗事半功倍

总结：简单来说，数据结构，就是一种程序设计优化的方法论，研究数据的 逻辑结构 和 物理结构 以及它们之间相互关系，并对这种结构定义相应的 运算 ，目的是加快程序的执行速度、减少内存占用的空间。

具体研究对象如下：

# 1.1 研究对象一：数据的逻辑结构

数据的逻辑结构指反映数据元素之间的逻辑关系，而与数据的存储无关，是独立于计算机的。

集合结构：数据结构中的元素之间除了 “ 同属一个集合 ” 的相互关系外，别无其他关系。集合元素之间没有逻辑关系。
线性结构：数据结构中的元素存在 一对一 的相互关系。比如：排队。结构中必须存在唯一的首元素和唯一的尾元素。体现为：一维数组、链表、栈、队列
树形结构：数据结构中的元素存在 一对多 的相互关系。比如：家谱、文件系统、组织架构
图形结构：数据结构中的元素存在 多对多 的相互关系。比如：全国铁路网、地铁图

# 1.2 研究对象二：数据的存储结构（或物理结构）

数据的物理结构 / 存储结构：包括 数据元素的表示 和 关系的表示 。数据的存储结构是逻辑结构用计算机语言的实现，它依赖于计算机语言。

结构 1：顺序结构

顺序结构就是使用一组 连续的存储单元 依次存储逻辑上相邻的各个元素。
优点：
- 只需要申请存放数据本身的内存空间即可
- 支持下标访问，也可以实现随机访问
缺点：
- 必须静态分配连续空间，内存空间的利用率比较低
- 插入或删除可能需要移动大量元素，效率比较低

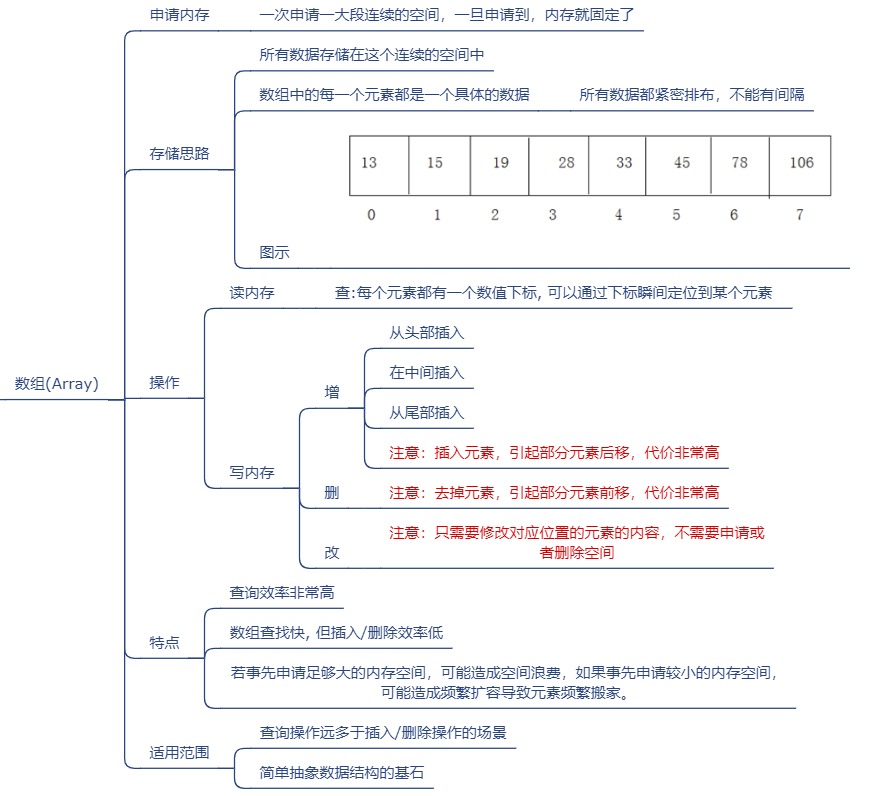
结构 2：链式结构

不使用连续的存储空间存放结构的元素，而是为每一个元素构造一个节点。 节点 中除了存放 数据 本身以外，还需要存放指向下一个节点的 指针 。
优点：
- 不采用连续的存储空间导致内存空间利用率比较高，克服顺序存储结构中预知元素个数的缺点
- 插入或删除元素时，不需要移动大量的元素
缺点：
- 需要额外的空间来表达数据之间的逻辑关系
- 不支持下标访问和随机访问，只能遍历各个节点去访问

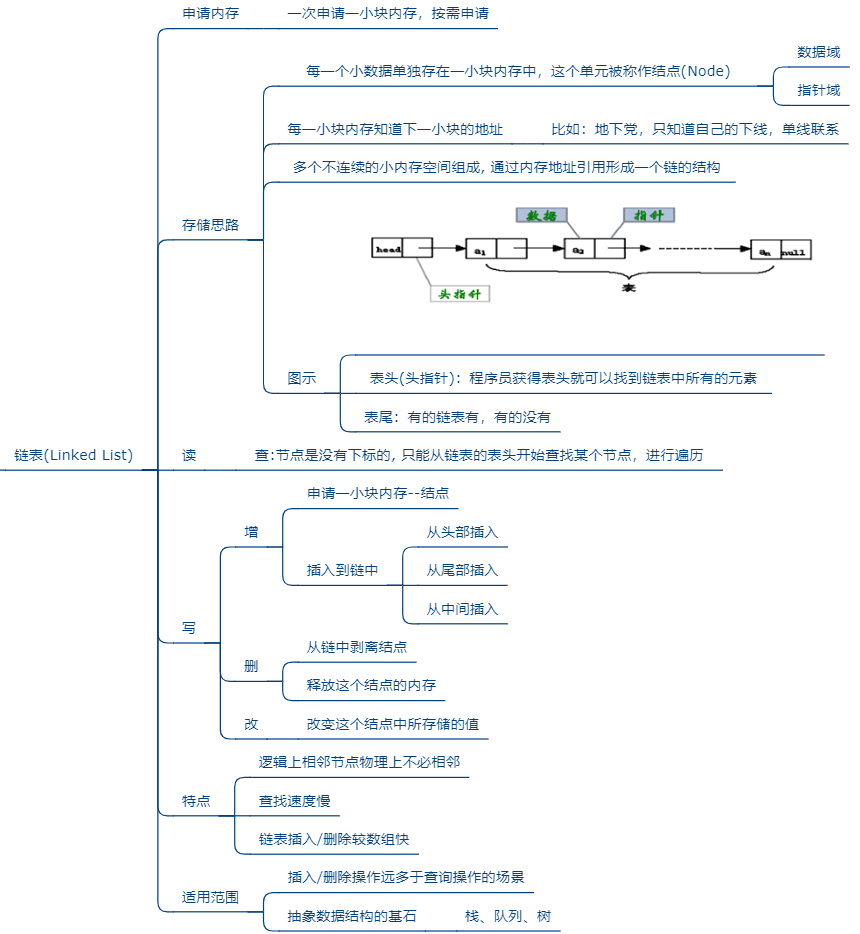
结构 3：索引结构

除建立存储 节点 信息外，还建立附加的 ** 索引表 ** 来记录每个元素节点的地址。索引表由若干索引项组成。 索引项 的一般形式是：（关键字，地址）。
优点：用节点的索引号来确定结点存储地址，检索速度快。
缺点：
- 增加了附加的索引表，会占用较多的存储空间
- 在增加和删除数据时要修改索引表，因而会花费较多的时间

结构 4：散列结构

根据元素的关键字直接计算出该元素的存储地址，又称为 Hash存储 。
优点：检索、增加和删除结点的操作都很快。
缺点：
- 不支持排序
- 一般比用线性表存储需要更多的空间
- 并且记录的关键字不能重复

# 1.3 研究对象三：运算结构

施加在数据上的运算包括运算的定义和实现。运算的定义是针对逻辑结构的，指出运算的功能；运算的实现是针对存储结构的，指出运算的具体操作步骤。

分配资源，建立结构，释放资源
插入和删除
获取和遍历
修改和排序

# 1.4 小结

开发中习惯如下理解逻辑结构：

线性表（一对一）
- 数组
- 链表
- 栈
- 队列
树（一对多）
- 二叉树
- 多路查找树
- 堆
- 其他
图（多对多）
哈希表：HashSet、HashMap

数据结构分类：

真实数据结构
- 线性表（顺序表）：数组（Array）、ArrayList
- 线性表（链表）：LinkedList
抽象数据结构（ADT）
基于真实数据结构（数组 / 链表）来实现
- 栈（基于数组 / 链表）
- 队列（基于数组 / 链表）
- 树
- 图
- 其他（散列表、堆）

# 2. 一维数组

# 2.1 数组的特点

在 Java 中，数组是用来存放同一种数据类型的集合，注意只能存放同一种数据类型。

	// 只声明了类型和长度
	数据类型[] 数组名称 = new 数据类型[数组长度];

	// 声明了类型，初始化赋值，大小由元素个数决定
	数据类型[] 数组名称 = {数组元素1，数组元素2，......}

例如：整型数组

例如：对象数组

逻辑结构：线性结构
物理结构特点：一次申请一大段连续的空间，一旦申请到了，内存就固定了。
优点：查找数据快，因为通过下标可快速定位某个元素
缺点：
- 不能动态扩展(初始化给大了，浪费；给小了，不够用)
- 插入、删除数据慢，因为要移动大量数据
适用场景：查询操作远多于插入 / 删除操作的场景
具体的，如下图：

# 2.2 自定义数组

	package com.atguigu01.overview.array;

	/**
	* @author 尚硅谷 - 宋红康
	* @create 14:39
	*/
	class Array {
	private Object[] elementData;

	private int size;

	public Array(int capacity){
	elementData = new Object[capacity];
	}

	/**
	* 添加元素
	* @param value
	*/
	public void add(Object value){
	if(size >= elementData.length){
	throw new RuntimeException("数组已满，不可添加");
	}
	elementData[size] = value;
	size++;
	}

	/**
	* 查询元素 value 在数组中的索引位置
	* @param value
	* @return
	*/
	public int find(Object value){
	for (int i = 0; i < size; i++) {
	if(elementData[i].equals(value)){
	return i;
	}
	}
	return -1;
	}

	/**
	* 从当前数组中移除首次出现的 value 元素
	* @param value
	* @return
	*/
	public boolean delete(Object value){
	int index = find(value);
	if(index == -1){
	return false;
	}

	for(int i = index;i < size - 1;i++){
	elementData[i] = elementData[i + 1];
	}
	elementData[size - 1] = null;
	size--;
	return true;
	}

	/**
	* 将数组中首次出现的 oldValue 替换为 newValue
	* @param oldValue
	* @param newValue
	* @return
	*/
	public boolean update(Object oldValue,Object newValue){
	int index = find(oldValue);
	if(index == -1){
	return false;
	}
	elementData[index] = newValue;
	return true;

	}

	/**
	* 遍历数组中所有数据
	*/
	public void print(){
	System.out.print("{");
	for (int i = 0; i < size; i++) {
	if(i == size - 1){
	System.out.println(elementData[i] + "}");
	break;
	}
	System.out.print(elementData[i] + ",");
	}
	}
	}

	// 测试类
	public class ArrayTest {
	public static void main(String[] args) {
	Array arr = new Array(10);

	arr.add(123);
	arr.add("AA");
	arr.add(345);
	arr.add(345);
	arr.add("BB");

	arr.delete(345);

	arr.update(345,444);

	arr.print();
	}
	}

# 3. 链表

# 3.1 链表的特点

逻辑结构：线性结构
物理结构特点：
- 不要求存储空间连续
- 不需要提前声明内存大小
存储特点：链表由一系列结点 node（链表中每一个元素称为 ** 结点 **）组成，可以在代码执行过程中动态创建结点。每个结点包括两个部分：一个是存储数据元素的 数据域 ，另一个是存储下一个结点地址的 指针域 。

优点
- 节省内存空间
- 插入、删除数据快，只需要修改指针即可，不需要移动大量数据
缺点：必须按顺序逐个查找数据，麻烦
使用场景：插入 / 删除操作远多于查询操作的场景
常见的链表结构有如下的形式：

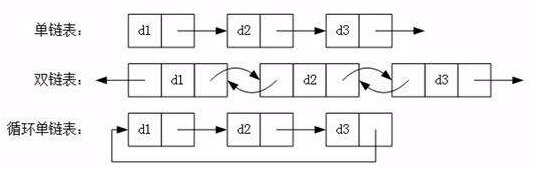
1563448858180

# 3.2 自定义链表

# 3.2.1 自定义单向链表

	/*
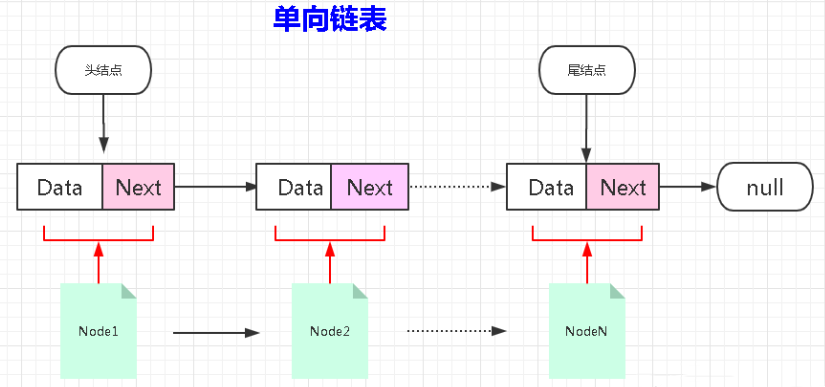
	单链表中的节点。
	节点是单向链表中基本的单元。
	每一个节点 Node 都有两个属性：
	一个属性：是存储的数据。
	另一个属性：是下一个节点的内存地址。
	*/
	public class Node {

	// 存储的数据
	Object data;

	// 下一个节点的内存地址
	Node next;

	public Node(){

	}

	public Node(Object data, Node next){
	this.data = data;
	this.next = next;
	}
	}

	/*
	链表类 (单向链表)
	*/
	public class Link<E> {

	// 头节点
	Node header;

	private int size = 0;

	public int size(){
	return size;
	}

	// 向链表中添加元素的方法（向末尾添加）
	public void add(E data){
	//public void add(Object data){
	// 创建一个新的节点对象
	// 让之前单链表的末尾节点 next 指向新节点对象。
	// 有可能这个元素是第一个，也可能是第二个，也可能是第三个。
	if(header == null){
	// 说明还没有节点。
	//new 一个新的节点对象，作为头节点对象。
	// 这个时候的头节点既是一个头节点，又是一个末尾节点。
	header = new Node(data, null);
	}else {
	// 说明头不是空！
	// 头节点已经存在了！
	// 找出当前末尾节点，让当前末尾节点的 next 是新节点。
	Node currentLastNode = findLast(header);
	currentLastNode.next = new Node(data, null);
	}
	size++;
	}

	/**
	* 专门查找末尾节点的方法。
	*/
	private Node findLast(Node node) {
	if(node.next == null) {
	// 如果一个节点的 next 是 null
	// 说明这个节点就是末尾节点。
	return node;
	}
	// 程序能够到这里说明：node 不是末尾节点。
	return findLast(node.next); // 递归算法！
	}

	/*// 删除链表中某个数据的方法
	public void remove (Object obj){
	// 略
	}

	// 修改链表中某个数据的方法
	public void modify (Object newObj){
	// 略
	}

	// 查找链表中某个元素的方法。
	public int find (Object obj){
	// 略
	}*/
	}

# 3.2.2 自定义双向链表

	/*
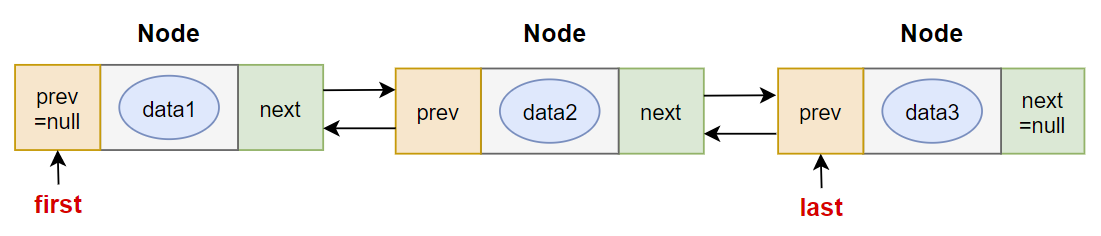
	双向链表中的节点。
	*/
	public class Node<E> {
	Node prev;
	E data;
	Node next;

	Node(Node prev, E data, Node next) {
	this.prev = prev;
	this.data = data;
	this.next = next;
	}
	}

	/**
	* 链表类 (双向链表)
	* @author 尚硅谷 - 宋红康
	* @create 15:05
	*/
	public class MyLinkedList<E> implements Iterable<E>{
	private Node first; // 链表的首元素
	private Node last; // 链表的尾元素
	private int total;

	public void add(E e){
	Node newNode = new Node(last, e, null);

	if(first == null){
	first = newNode;
	}else{
	last.next = newNode;
	}
	last = newNode;
	total++;
	}

	public int size(){
	return total;
	}

	public void delete(Object obj){
	Node find = findNode(obj);
	if(find != null){
	if(find.prev != null){
	find.prev.next = find.next;
	}else{
	first = find.next;
	}
	if(find.next != null){
	find.next.prev = find.prev;
	}else{
	last = find.prev;
	}

	find.prev = null;
	find.next = null;
	find.data = null;

	total--;
	}
	}

	private Node findNode(Object obj){
	Node node = first;
	Node find = null;

	if(obj == null){
	while(node != null){
	if(node.data == null){
	find = node;
	break;
	}
	node = node.next;
	}
	}else{
	while(node != null){
	if(obj.equals(node.data)){
	find = node;
	break;
	}
	node = node.next;
	}
	}
	return find;
	}

	public boolean contains(Object obj){
	return findNode(obj) != null;
	}

	public void update(E old, E value){
	Node find = findNode(old);
	if(find != null){
	find.data = value;
	}
	}

	@Override
	public Iterator<E> iterator() {
	return new Itr();
	}

	private class Itr implements Iterator<E>{
	private Node<E> node = first;

	@Override
	public boolean hasNext() {
	return node!=null;
	}

	@Override
	public E next() {
	E value = node.data;
	node = node.next;
	return value;
	}
	}
	}

自定义双链表测试：

	package com.atguigu.list;

	public class MyLinkedListTest {
	public static void main(String[] args) {
	MyLinkedList<String> my = new MyLinkedList<>();
	my.add("hello");
	my.add("world");
	my.add(null);
	my.add(null);
	my.add("java");
	my.add("java");
	my.add("atguigu");

	System.out.println("一共有：" + my.size());
	System.out.println("所有元素：");
	for (String s : my) {
	System.out.println(s);
	}
	System.out.println("-------------------------------------");
	System.out.println("查找java,null,haha的结果：");
	System.out.println(my.contains("java"));
	System.out.println(my.contains(null));
	System.out.println(my.contains("haha"));

	System.out.println("-------------------------------------");
	System.out.println("替换java,null后：");
	my.update("java","JAVA");
	my.update(null,"songhk");
	System.out.println("所有元素：");
	for (String s : my) {
	System.out.println(s);
	}
	System.out.println("-------------------------------------");
	System.out.println("删除hello，JAVA,null，atguigu后：");
	my.delete("hello");
	my.delete("JAVA");
	my.delete(null);
	my.delete("atguigu");
	System.out.println("所有元素：");
	for (String s : my) {
	System.out.println(s);
	}
	}
	}

# 4. 栈

# 4.1 栈的特点

栈（Stack）又称为堆栈或堆叠，是限制 仅在表的一端（栈顶）进行插入、删除运算的线性表 。
栈按照 先进后出(FILO,first in last out) 的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶。每次删除（退栈）的总是删除当前栈中最后插入（进栈）的元素，而最先插入的是被放在栈的底部，要到最后才能删除。
核心类库中的栈结构有 Stack 和 LinkedList。
- Stack 就是顺序栈，它是 java.util.Vector 的子类。
- LinkedList 是链式栈。
体现栈结构的操作方法：
- push(E e) 方法：压入栈
- pop() 方法：弹出栈
- peek() 方法：查看栈顶元素，不弹出
- search(Object obj)：查找元素出现位置
- clear()：清栈
- size()：大小
- empty()：判断是否是空
时间复杂度:
- 索引: O(n)
- 搜索: O(n)
- 插入: O(1)
- 移除: O(1)
使用场景：
- 二叉树、森林的遍历
- CPU 的中断处理
- 图形的深度优先查找法 (DFS)
- 递归调用
  - 斐波那契数列
  - 汉诺塔问题
- 子程序的调用
图示：

# 4.2 Stack 使用举例

	/**
	* @author 尚硅谷 - 宋红康
	* @create 15:44
	*/
	public class TestStack {
	/*
	* 测试 Stack
	* */
	@Test
	public void test1(){
	Stack<Integer> list = new Stack<>();
	list.push(1);
	list.push(2);
	list.push(3);

	System.out.println("list = " + list);

	System.out.println("list.peek()=" + list.peek());
	System.out.println("list.peek()=" + list.peek());
	System.out.println("list.peek()=" + list.peek());

	/*
	System.out.println("list.pop() =" + list.pop());
	System.out.println("list.pop() =" + list.pop());
	System.out.println("list.pop() =" + list.pop());
	System.out.println("list.pop() =" + list.pop());//java.util.NoSuchElementException
	*/

	while(!list.empty()){
	System.out.println("list.pop() =" + list.pop());
	}
	}

	/*
	* 测试 LinkedList
	* */
	@Test
	public void test2(){
	LinkedList<Integer> list = new LinkedList<>();
	list.push(1);
	list.push(2);
	list.push(3);

	System.out.println("list = " + list);

	System.out.println("list.peek()=" + list.peek());
	System.out.println("list.peek()=" + list.peek());
	System.out.println("list.peek()=" + list.peek());

	/*
	System.out.println("list.pop() =" + list.pop());
	System.out.println("list.pop() =" + list.pop());
	System.out.println("list.pop() =" + list.pop());
	System.out.println("list.pop() =" + list.pop());//java.util.NoSuchElementException
	*/
	while(!list.isEmpty()){
	System.out.println("list.pop() =" + list.pop());
	}
	}
	}

# 4.3 自定义栈

	public class MyStack {
	// 向栈当中存储元素，我们这里使用一维数组模拟。存到栈中，就表示存储到数组中。
	// 为什么选择 Object 类型数组？因为这个栈可以存储 java 中的任何引用类型的数据
	private Object[] elements;

	// 栈帧，永远指向栈顶部元素
	// 那么这个默认初始值应该是多少。注意：最初的栈是空的，一个元素都没有。
	//private int index = 0; // 如果 index 采用 0，表示栈帧指向了顶部元素的上方。
	//private int index = -1; // 如果 index 采用 - 1，表示栈帧指向了顶部元素。
	private int index;

	/**
	* 无参数构造方法。默认初始化栈容量 10.
	*/
	public MyStack() {
	// 一维数组动态初始化
	// 默认初始化容量是 10.
	this.elements = new Object[10];
	// 给 index 初始化
	this.index = -1;
	}

	/**
	* 压栈的方法
	* @param obj 被压入的元素
	*/
	public void push(Object obj) throws Exception {
	if(index >= elements.length - 1){
	// 方式 1：
	//System.out.println ("压栈失败，栈已满！");
	//return;
	// 方式 2：
	throw new Exception("压栈失败，栈已满！");
	}
	// 程序能够走到这里，说明栈没满
	// 向栈中加 1 个元素，栈帧向上移动一个位置。
	index++;
	elements[index] = obj;
	System.out.println("压栈" + obj + "元素成功，栈帧指向" + index);
	}

	/**
	* 弹栈的方法，从数组中往外取元素。每取出一个元素，栈帧向下移动一位。
	* @return
	*/
	public Object pop() throws Exception {
	if (index < 0) {
	// 方式 1：
	//System.out.println ("弹栈失败，栈已空！");
	//return;
	// 方式 2：
	throw new Exception("弹栈失败，栈已空！");
	}
	// 程序能够执行到此处说明栈没有空。
	Object obj = elements[index];
	System.out.print("弹栈" + obj + "元素成功，");
	elements[index] = null;
	// 栈帧向下移动一位。
	index--;
	return obj;
	}

	//set 和 get 也许用不上，但是你必须写上，这是规矩。你使用 IDEA 生成就行了。
	// 封装：第一步：属性私有化，第二步：对外提供 set 和 get 方法。
	public Object[] getElements() {
	return elements;
	}

	public void setElements(Object[] elements) {
	this.elements = elements;
	}

	public int getIndex() {
	return index;
	}

	public void setIndex(int index) {
	this.index = index;
	}
	}

# 5. 队列

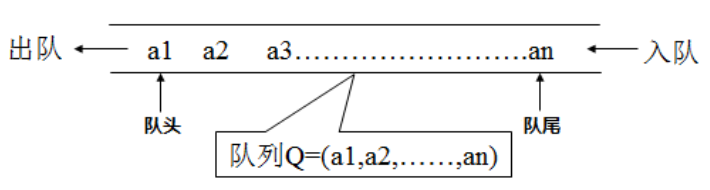
队列（Queue）是 只允许在一端进行插入，而在另一端进行删除的运算受限的线性表 。
队列是逻辑结构，其物理结构可以是数组，也可以是链表。
队列的修改原则：队列的修改是依 先进先出（FIFO）的原则 进行的。新来的成员总是加入队尾（即不允许 "加塞"），每次离开的成员总是队列头上的（不允许中途离队），即当前 "最老的" 成员离队。
操作方法：
- 加入元素到队列尾部: add(object obj)/offer(object obj)
- 获取队列头部元素，不删除该元素:element()/peek()
- 获取队列头部元素，并删除该元素:remove()/poll()
- 清理队列: clear()
- 得到队列的大小: size()
- 判断队列是否是空的: isEmpty()
使用场景：
- 图形的广度优先查找法 (BFS)
- 可用于计算机各种事件处理的模拟
  - 如：事件队列，消息队列
- CPU 的作业调度
图示：

# 6. 树与二叉树

# 6.1 树的理解

专有名词解释：

结点 ：树中的数据元素都称之为结点

根节点 ：最上面的结点称之为根，一颗树只有一个根且由根发展而来，从另外一个角度来说，每个结点都可以认为是其子树的根

父节点 ：结点的上层结点，如图中，结点 K 的父节点是 E、结点 L 的父节点是 G

子节点 ：节点的下层结点，如图中，节点 E 的子节点是 K 节点、节点 G 的子节点是 L 节点

兄弟节点 ：具有相同父节点的结点称为兄弟节点，图中 F、G、H 互为兄弟节点

结点的度数 ：每个结点所拥有的子树的个数称之为结点的度，如结点 B 的度为 3

树叶（或叶子结点） ：度数为 0 的结点，也叫作终端结点，图中 D、K、F、L、H、I、J 都是树叶

非终端节点（或分支节点） ：树叶以外的节点，或度数不为 0 的节点。图中根、A、B、C、E、G 都是

树的深度（或高度） ：树中结点的最大层次数，图中树的深度为 4

结点的层数 ：从根节点到树中某结点所经路径上的分支树称为该结点的层数，根节点的层数规定为 1，其余结点的层数等于其父亲结点的层数 + 1

同代 ：在同一棵树中具有相同层数的节点

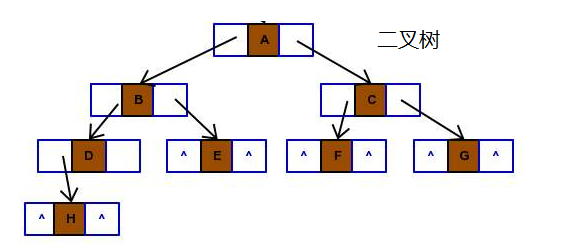
# 6.2 二叉树的基本概念

二叉树（Binary tree）是树形结构的一个重要类型。二叉树特点是 每个结点最多只能有两棵子树 ，且 有左右之分 。许多实际问题抽象出来的数据结构往往是二叉树形式，二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。

1563449427345

# 6.3 二叉树的遍历

前序遍历：中左右（根左右）
即先访问根结点，再前序遍历左子树，最后再前序遍历右子树。前序遍历运算访问二叉树各结点是以根、左、右的顺序进行访问的。
中序遍历：左中右（左根右）
即先中前序遍历左子树，然后再访问根结点，最后再中序遍历右子树。中序遍历运算访问二叉树各结点是以左、根、右的顺序进行访问的。
后序遍历：左右中（左右根）
即先后序遍历左子树，然后再后序遍历右子树，最后访问根结点。后序遍历运算访问二叉树各结点是以左、右、根的顺序进行访问的。

前序遍历：ABDHIECFG

中序遍历：HDIBEAFCG

后序遍历：HIDEBFGCA

# 6.4 经典二叉树

1、 满二叉树 ：除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。第 n 层的结点数是 2^n-1，总的结点个数是 2ⁿ-1。

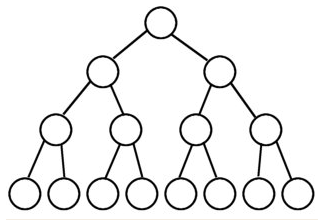
1574575163883

2、 完全二叉树 ：叶子结点只能出现在最底层的两层，且 **最底层叶结点均处于次底层叶结点的左侧**。

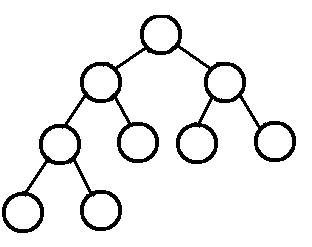
1574575180247

3、 二叉搜索/排序树 ：即为 BST (binary search/sort tree)。满足如下性质：
（1）若它的左子树不为空，则左子树上所有结点的值均小于它的根节点的值；
（2）若它的右子树不为空，则右子树上所有结点的值均大于它的根节点的值；
（3）它的左、右子树也分别为二叉搜索 / 排序树。

对二叉查找树进行中序遍历，得到有序集合。便于检索。

4、 平衡二叉树 ：（Self-balancing binary search tree， AVL ）首先是二叉排序树，此外具有以下性质：
（1）它是一棵空树或它的 **左右两个子树的高度差的绝对值不超过 1**
（2）并且 **左右两个子树也都是一棵平衡二叉树**
（3）非叶节点不要求有两个子结点

平衡二叉树的目的是为了减少二叉查找树的层次，提高查找速度。
平衡二叉树的常用实现有替罪羊树、Treap、伸展树等。

6、 红黑树 ：即 Red-Black Tree。 首先是二叉排序树 ，红黑树的每个节点上都有存储位表示节点的颜色，可以是红 (Red) 或黑 (Black)。

红黑树是在计算机科学中用到的一种数据结构，它是在 1972 年由 Rudolf Bayer 发明的。红黑树是复杂的，但它的操作有着 良好的最坏情况运行时间 ，并且在 实践中是高效的 ：它 可以在O(log n)时间内做查找，插入和删除 ，这里的 n 是树中元素的数目。

红黑树的特性：

每个节点是红色或者黑色
根节点是黑色
每个叶子节点（NIL）是黑色。（注意：这里叶子节点，是指为空 (NIL 或 NULL) 的叶子节点）
每个红色节点的两个子节点都是黑色的。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

推论：从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点（确保没有一条路径会比其他路径长出 2 倍）

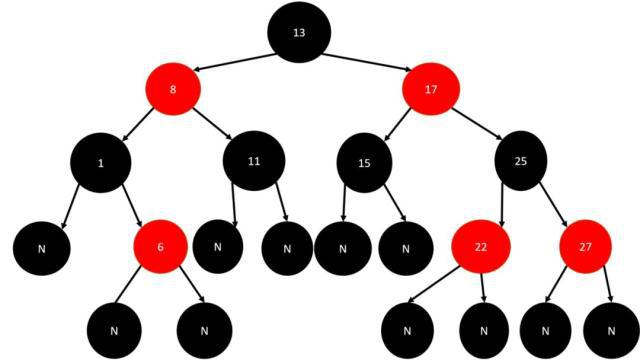
当我们插入或删除节点时，可能会破坏已有的红黑树，使得它不满足以上 5 个要求，那么此时就需要进行 维护 ，使得它继续满足以上的 5 个要求：

1、 recolor ：将某个节点变红或变黑

2、 rotation ：将红黑树某些结点分支进行旋转（左旋或右旋）

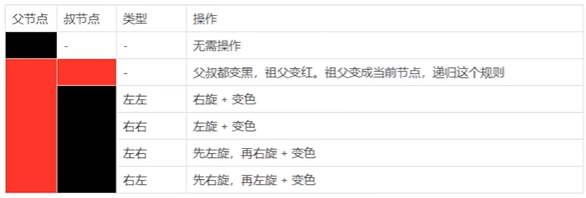
红黑树可以通过红色节点和黑色节点尽可能的保证二叉树的平衡。主要是用它来存储有序的数据，它的时间复杂度是O(logN)，效率非常之高。

# 6.5 二叉树及其结点的表示

普通二叉树：

	public class BinaryTree<E>{
	private TreeNode root; // 二叉树的根结点
	private int total;// 结点总个数

	private class TreeNode{
	// 至少有以下几个部分
	TreeNode parent;
	TreeNode left;
	E data;
	TreeNode right;

	public TreeNode(TreeNode parent, TreeNode left, E data, TreeNode right) {
	this.parent = parent;
	this.left = left;
	this.data = data;
	this.right = right;
	}
	}
	}

TreeMap 红黑树：

	public class TreeMap<K,V> {
	private transient Entry<K,V> root;
	private transient int size = 0;

	static final class Entry<K,V> implements Map.Entry<K,V> {
	K key;
	V value;
	Entry<K,V> left;
	Entry<K,V> right;
	Entry<K,V> parent;
	boolean color = BLACK;

	/**
	* Make a new cell with given key, value, and parent, and with
	* {@code null} child links, and BLACK color.
	*/
	Entry(K key, V value, Entry<K,V> parent) {
	this.key = key;
	this.value = value;
	this.parent = parent;
	}
	}
	}

# 7. List 接口分析

List 接口的实现类	ArrayList	~~Vector~~	LinkedList
地位	新版的动态数组	旧版的动态数组	链表
底层实现	Object 数组，但可以扩容	Object 数组	双向链表
默认的初始容量	JDK6.0 及之前是 10；JDK8.0 之后是 `0` ，之后在添加第一个元素时，再创建长度为 10 的数组	`10`	0
扩容机制	默认扩容为原来的 `1.5倍`	默认扩容增加为原来的 `2倍`	不需要扩容
特点	线程不安全、效率高	线程安全、效率低	线程不安全
使用场景	频繁追加、查找数据	避免使用	频繁插入、删除数据
说明	对于频繁访问列表中的某一个元素，只需要在列表末尾进行添加和删除元素操作的情况下		元素是通过指针相互连接的，在插入 / 删除元素时，只需要改动前后元素的指针即可

# 7.1 List 接口特点

List 集合所有的元素是以一种 线性方式 进行存储的，例如，存元素的顺序是 11、22、33。那么集合中，元素的存储就是按照 11、22、33 的顺序完成的）。
它是一个元素 存取有序 的集合。即元素的存入顺序和取出顺序有保证。
集合中的元素是 可重复 的，通过元素的 equals 方法，来比较是否为重复的元素。

1563549818689

注意：
List 集合关心元素是否有序，而不关心是否重复，请大家记住这个原则。例如 “张三” 可以领取两个号。

List 接口的主要实现类
- ArrayList：动态数组
- Vector：动态数组
  - Stack：栈
- LinkedList：双向链表

# 7.2 动态数组 ArrayList 与 Vector

Java 的 List 接口的实现类中有两个动态数组的实现：ArrayList 和 Vector。

# 7.2.1 ArrayList 与 Vector 的区别

它们的底层物理结构都是 Object[]数组 ，我们称为 动态数组 。

	ArrayList	Vector
特点	新版的动态数组， `线程不安全` ， `效率高`	旧版的动态数组， `线程安全` ， `效率低`
默认的初始容量	JDK6.0 及之前是 10；JDK8.0 之后是 `0` ，之后在添加第一个元素时，再创建长度为 10 的数组	`10`
扩容机制	默认扩容为原来的 `1.5倍`	默认扩容增加为原来的 `2倍`

JDK8.0 后，ArrayList 的容量初始化机制：
用的时候，再创建数组，避免浪费。因为很多方法的返回值是 ArrayList 类型，需要返回一个 ArrayList 的对象，例如：后期从数据库查询对象的方法，返回值很多就是 ArrayList。有可能你要查询的数据不存在，要么返回 null，要么返回一个没有元素的 ArrayList 对象。

# 7.2.2 ArrayList 部分源码分析

JDK1.7 和 JDK1.8 中 ArrayList 的源码区别：

数组初始化机制不同
在 JDK1.8 中，如果不指定长度，使用无参构造方法 ArrayList list = new ArrayList() 创建 List 集合时，底层的 Object[] elementData 初始化为 {} （空的数组），并没有直接创建长度为 10 的数组。
只有在 首次添加元素 时，才会创建长度为 10 的 Object [] 数组。
并且随着元素的添加，当要添加第 11 个元素时，底层的数组已满，需要扩容， 默认扩容到原来的1.5倍 ，并将原数组中的元素通过 Arrays.copyOf(原数组,新容量) 方法复制，其余元素默认为 0/null，返回值为新数组。

# JDK1.7.0_07

类似于单例设计模式中的 饿汉式

举例：

	/**
	* 测试 jdk1.7 中的 ArrayList 初始化、添加元素、扩容
	* 底层的物理结构：一个 Object [] 数组，默认容量 DEFAULT_CAPACITY = 10，实际存储的元素个数 size
	*/
	@Test
	public void test1() {
	//↓ 底层创建了一个长度为 10 的 Object [] 数组 elementData：：Object [] elementData = new Object [10];
	ArrayList list = new ArrayList();
	list.add("AA"); //elementData[0] = "AA";
	list.add("BB"); //elementData[1] = "BB";
	//... 当添加第 11 个元素时，数组已满，默认扩容为原来的 1.5 倍，并将原数组中的元素复制到新数组中
	//elementData = Arrays.copyOf (elementData, newCapacity); 参数分别是原数组、新数组的长度
	}

源码：

	// 属性
	private transient Object[] elementData; // 存储底层数组元素
	private int size; // 记录数组中实际存储的元素的个数

	// 构造器
	public ArrayList() {
	this(10); // 指定初始容量为 10
	}

	public ArrayList(int initialCapacity) {
	super();
	// 检查初始容量的合法性
	if (initialCapacity < 0)
	throw new IllegalArgumentException("Illegal Capacity: "+ initialCapacity);
	// 数组初始化为长度为 initialCapacity 的数组
	this.elementData = new Object[initialCapacity];
	}

	// 方法：add () 相关方法
	public boolean add(E e) {
	ensureCapacityInternal(s ize + 1); // 查看当前数组是否够多存一个元素
	elementData[size++] = e; // 将元素 e 添加到 elementData 数组中
	return true;
	}

	private void ensureCapacityInternal(int minCapacity) {
	modCount++;
	// 如果 if 条件满足，则进行数组的扩容
	if (minCapacity - elementData.length > 0)
	grow(minCapacity);
	}

	private void grow(int minCapacity) {
	// overflow-conscious code
	int oldCapacity = elementData.length; // 当前数组容量
	int newCapacity = oldCapacity + (oldCapacity >> 1); // 新数组容量是旧数组容量的 1.5 倍
	if (newCapacity - minCapacity < 0) // 判断旧数组的 1.5 倍是否够
	newCapacity = minCapacity;
	// 判断旧数组的 1.5 倍是否超过最大数组限制
	if (newCapacity - MAX_ARRAY_SIZE > 0)
	newCapacity = hugeCapacity(minCapacity);
	// 复制一个新数组
	elementData = Arrays.copyOf(elementData, newCapacity);
	}

	// 方法：remove () 相关方法
	public E remove(int index) {
	rangeCheck(index); // 判断 index 是否在有效的范围内

	modCount++; // 修改次数加 1
	// 取出 [index] 位置的元素，[index] 位置的元素就是要被删除的元素，用于最后返回被删除的元素
	E oldValue = elementData(index);

	int numMoved = size - index - 1; // 确定要移动的次数
	// 如果需要移动元素，就用 System.arraycopy 移动元素
	if (numMoved > 0)
	System.arraycopy(elementData, index+1, elementData, index, numMoved);
	// 将 elementData [size-1] 位置置空，让 GC 回收空间，元素个数减少
	elementData[--size] = null;

	return oldValue;
	}

	private void rangeCheck(int index) {
	if (index >= size) //index 不合法的情况
	throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
	}

	E elementData(int index) { // 返回指定位置的元素
	return (E) elementData[index];
	}

	// 方法：set () 方法相关
	public E set(int index, E element) {
	rangeCheck(index); // 检验 index 是否合法

	// 取出 [index] 位置的元素，[index] 位置的元素就是要被替换的元素，用于最后返回被替换的元素
	E oldValue = elementData(index);
	// 用 element 替换 [index] 位置的元素
	elementData[index] = element;
	return oldValue;
	}

	// 方法：get () 相关方法
	public E get(int index) {
	rangeCheck(index); // 检验 index 是否合法

	return elementData(index); // 返回 [index] 位置的元素
	}

	// 方法：indexOf ()
	public int indexOf(Object o) {
	// 分为 o 是否为空两种情况
	if (o == null) {
	// 从前往后找
	for (int i = 0; i < size; i++)
	if (elementData[i]==null)
	return i;
	} else {
	for (int i = 0; i < size; i++)
	if (o.equals(elementData[i]))
	return i;
	}
	return -1;
	}

	// 方法：lastIndexOf ()
	public int lastIndexOf(Object o) {
	// 分为 o 是否为空两种情况
	if (o == null) {
	// 从后往前找
	for (int i = size-1; i >= 0; i--)
	if (elementData[i]==null)
	return i;
	} else {
	for (int i = size-1; i >= 0; i--)
	if (o.equals(elementData[i]))
	return i;
	}
	return -1;
	}

# jdk1.8.0_271

类似于单例设计模式中的 懒汉式

举例：

	/**
	* 测试 jdk1.8 中的 ArrayList 初始化、添加元素、扩容
	* 底层的物理结构：一个 Object [] 数组，默认容量 DEFAULT_CAPACITY = 10，实际存储的元素个数 size
	*/
	@Test
	public void test2() {
	//↓ 底层创建了一个长度为 0 的 Object [] 数组 elementData：Object [] elementData = {};
	ArrayList list = new ArrayList();
	list.add("AA"); // 首次添加元素时，会初始化数组：elementData = new Object [10]; elementData [0] = "AA";
	list.add("BB"); //elementData[1] = "BB";
	//... 当添加第 11 个元素时，数组已满，默认扩容为原来的 1.5 倍，并将原数组中的元素复制到新数组中
	//elementData = Arrays.copyOf (elementData, newCapacity); 参数分别是原数组、新数组的长度
	}

源码：

	// 属性
	transient Object[] elementData;
	private int size;
	private static final Object[] DEFAULTCAPACITY_EMPTY_ELEMENTDATA = {};

	// 构造器
	public ArrayList() {
	this.elementData = DEFAULTCAPACITY_EMPTY_ELEMENTDATA; // 初始化为空数组
	}

	// 方法:add () 相关方法
	public boolean add(E e) {
	// 查看当前数组是否够多存一个元素
	ensureCapacityInternal(size + 1); // Increments modCount!!
	// 存入新元素到 [size] 位置，然后 size 自增 1
	elementData[size++] = e;
	return true;
	}

	private void ensureCapacityInternal(int minCapacity) {
	ensureExplicitCapacity(calculateCapacity(elementData, minCapacity));
	}

	private static int calculateCapacity(Object[] elementData, int minCapacity) {
	// 如果当前数组还是空数组
	if (elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {
	// 那么 minCapacity 取 DEFAULT_CAPACITY 与 minCapacity 的最大值
	return Math.max(DEFAULT_CAPACITY, minCapacity);
	}
	return minCapacity;
	}

	// 查看是否需要扩容
	private void ensureExplicitCapacity(int minCapacity) {
	modCount++; // 修改次数加 1

	// 如果需要的最小容量比当前数组的长度大，即当前数组不够存，就扩容
	if (minCapacity - elementData.length > 0)
	grow(minCapacity);
	}

	private void grow(int minCapacity) {
	// overflow-conscious code
	int oldCapacity = elementData.length; // 当前数组容量
	int newCapacity = oldCapacity + (oldCapacity >> 1); // 新数组容量是旧数组容量的 1.5 倍
	// 看旧数组的 1.5 倍是否够
	if (newCapacity - minCapacity < 0)
	newCapacity = minCapacity;
	// 看旧数组的 1.5 倍是否超过最大数组限制
	if (newCapacity - MAX_ARRAY_SIZE > 0)
	newCapacity = hugeCapacity(minCapacity);
	// 复制一个新数组
	elementData = Arrays.copyOf(elementData, newCapacity);
	}

# 7.2.3 ArrayList 相关方法图示

ArrayList 采用数组作为底层实现

ArrayList 自动扩容过程

ArrayList 的 add (E e) 方法

ArrayList 的 add (int index,E e) 方法

# 7.2.4 Vector 部分源码分析

jdk1.8.0_271 中：

数组的 初始化容量即为10 ， 默认扩容为原来的2倍 。

举例：

	/**
	* 测试 jdk1.8 中 Vector 初始化、添加元素、扩容
	* 底层的物理结构：一个 Object [] 数组，默认容量 10，实际存储的元素个数 elementCount
	*/
	@Test
	public void test3() {
	//↓ 底层创建了一个长度为 10 的 Object [] 数组 elementData：elementData = new Object [10];
	Vector vec = new Vector();
	vec.add("AA"); //elementData[0] = "AA";
	vec.add("BB"); //elementData[1] = "BB";
	//... 当添加第 11 个元素时，数组已满，默认扩容为原来的 2 倍，并将原数组中的元素复制到新数组中
	//elementData = Arrays.copyOf(elementData, newCapacity);
	}

源码：

	// 属性
	protected Object[] elementData;
	protected int elementCount;

	// 构造器
	public Vector() {
	this(10); // 指定初始容量 initialCapacity 为 10
	}

	public Vector(int initialCapacity) {
	this(initialCapacity, 0); // 指定 capacityIncrement 增量为 0
	}

	public Vector(int initialCapacity, int capacityIncrement) {
	super();
	// 判断了形参初始容量 initialCapacity 的合法性
	if (initialCapacity < 0)
	throw new IllegalArgumentException("Illegal Capacity: "+ initialCapacity);
	// 创建了一个 Object [] 类型的数组
	this.elementData = new Object[initialCapacity];
	// 增量，默认是 0，如果是 0，后面就按照 2 倍增加，如果不是 0，后面就按照你指定的增量进行增量
	this.capacityIncrement = capacityIncrement;
	}

	// 方法：add () 相关方法
	//synchronized 意味着线程安全的
	public synchronized boolean add(E e) {
	modCount++;
	// 看是否需要扩容
	ensureCapacityHelper(elementCount + 1);
	// 把新的元素存入 [elementCount]，存入后，elementCount 元素的个数增 1
	elementData[elementCount++] = e;
	return true;
	}

	private void ensureCapacityHelper(int minCapacity) {
	// 看是否超过了当前数组的容量
	if (minCapacity - elementData.length > 0)
	grow(minCapacity); // 扩容
	}

	private void grow(int minCapacity) {
	// overflow-conscious code
	int oldCapacity = elementData.length; // 获取目前数组的长度
	// 如果 capacityIncrement 增量是 0，新容量 = oldCapacity 的 2 倍
	// 如果 capacityIncrement 增量是不是 0，新容量 = oldCapacity + capacityIncrement 增量；
	int newCapacity = oldCapacity + ((capacityIncrement > 0) ?
	capacityIncrement : oldCapacity);
	// 如果按照上面计算的新容量还不够，就按照你指定的需要的最小容量来扩容 minCapacity
	if (newCapacity - minCapacity < 0)
	newCapacity = minCapacity;
	// 如果新容量超过了最大数组限制，那么单独处理
	if (newCapacity - MAX_ARRAY_SIZE > 0)
	newCapacity = hugeCapacity(minCapacity);
	// 把旧数组中的数据复制到新数组中，新数组的长度为 newCapacity
	elementData = Arrays.copyOf(elementData, newCapacity);
	}

	// 方法：remove () 相关方法
	public boolean remove(Object o) {
	return removeElement(o);
	}
	public synchronized boolean removeElement(Object obj) {
	modCount++;
	// 查找 obj 在当前 Vector 中的下标
	int i = indexOf(obj);
	// 如果 i>=0，说明存在，删除 [i] 位置的元素
	if (i >= 0) {
	removeElementAt(i);
	return true;
	}
	return false;
	}

	// 方法：indexOf ()
	public int indexOf(Object o) {
	return indexOf(o, 0);
	}
	public synchronized int indexOf(Object o, int index) {
	if (o == null) {// 要查找的元素是 null 值
	for (int i = index ; i < elementCount ; i++)
	if (elementData[i]==null)// 如果是 null 值，用 ==null 判断
	return i;
	} else {// 要查找的元素是非 null 值
	for (int i = index ; i < elementCount ; i++)
	if (o.equals(elementData[i]))// 如果是非 null 值，用 equals 判断
	return i;
	}
	return -1;
	}

	// 方法：removeElementAt ()
	public synchronized void removeElementAt(int index) {
	modCount++;
	// 判断下标的合法性
	if (index >= elementCount) {
	throw new ArrayIndexOutOfBoundsException(index + " >= " +
	elementCount);
	}
	else if (index < 0) {
	throw new ArrayIndexOutOfBoundsException(index);
	}

	//j 是要移动的元素的个数
	int j = elementCount - index - 1;
	// 如果需要移动元素，就调用 System.arraycopy 进行移动
	if (j > 0) {
	// 把 index+1 位置以及后面的元素往前移动
	//index+1 的位置的元素移动到 index 位置，依次类推
	// 一共移动 j 个
	System.arraycopy(elementData, index + 1, elementData, index, j);
	}
	// 元素的总个数减少
	elementCount--;
	// 将 elementData [elementCount] 这个位置置空，用来添加新元素，位置的元素等着被 GC 回收
	elementData[elementCount] = null; /* to let gc do its work */
	}

# 7.3 链表 LinkedList

Java 中有双链表的实现：LinkedList，它是 List 接口的实现类。

LinkedList 是一个 双向链表 ，如图所示：

# 7.3.1 链表与动态数组的区别

	动态数组	链表
举例	ArrayList、Vector	LinkedList
底层物理结构	Object [] 数组	`双向链表`
性能	查找快，插入 / 删除慢	`查找慢` ， `插入/删除快`
扩容机制	扩容到 1.5/2 倍	不涉及扩容

动态数组
查找元素快，是因为可以根据 索引 访问。
插入 / 删除慢，是因为涉及到 移动元素 ，以及 扩容 问题。
链表
查找元素慢，是因为需要 从头开始逐个查找 。
插入 / 删除快，是因为只需要 修改前后元素的指向关系 即可，不需要移动元素，更不涉及扩容问题。

# 7.3.2 LinkedList 源码分析

jdk1.8.0_271 中：

举例：

	/**
	* 测试 jdk1.8 中 LinkedList 初始化、添加元素，不涉及扩容
	* 底层的物理结构：一个双向链表，默认容量 0，实际存储的元素个数 size，一个指向头 Node 的 first，一个指向尾 Node 的 last
	*/
	@Test
	public void test4() {
	LinkedList<String> list = new LinkedList<>();// 底层什么也没做
	//↓ 添加第一个元素时，会创建一个 Node 对象 1，其 prev 和 next 都为 null，但 List 对象的属性 first 和 last 都指向该 Node 对象 1
	list.add("AA");
	//↓ 添加第二个元素时，会创建一个 Node 对象 2，其 prev 指向 last 节点，而 last 节点的 next 指向该 Node 对象 2，构成双向链表
	// 该 Node 对象 2 的 next 为 null，但 List 对象的属性 last 指向该 Node 对象 2
	list.add("BB");
	//... 因为 LinkedList 是双向链表，所以添加元素时，不涉及扩容
	}

源码：

	// 属性
	transient Node<E> first; // 记录第一个结点的位置
	transient Node<E> last; // 记录当前链表的尾元素
	transient int size = 0; // 记录最后一个结点的位置

	// 构造器
	public LinkedList() {
	}

	// 其中，Node 类定义如下
	private static class Node<E> {
	E item; // 元素数据
	Node<E> next; // 下一个结点
	Node<E> prev; // 前一个结点

	Node(Node<E> prev, E element, Node<E> next) {
	this.item = element;
	this.next = next;
	this.prev = prev;
	}
	}

	// 方法：add () 相关方法
	public boolean add(E e) {
	linkLast(e); // 默认把新元素链接到链表尾部
	return true;
	}

	void linkLast(E e) {
	final Node<E> l = last; // 用 l 记录原来的最后一个结点
	// 创建新结点
	final Node<E> newNode = new Node<>(l, e, null);
	// 现在的新结点是最后一个结点了
	last = newNode;
	// 如果 l==null，说明原来的链表是空的
	if (l == null)
	// 那么新结点同时也是第一个结点
	first = newNode;
	else
	// 否则把新结点链接到原来的最后一个结点的 next 中
	l.next = newNode;
	// 元素个数增加
	size++;
	// 修改次数增加
	modCount++;
	}

	// 方法：获取 get () 相关方法
	public E get(int index) {
	checkElementIndex(index);
	return node(index).item;
	}

	// 方法：插入 add () 相关方法
	public void add(int index, E element) {
	checkPositionIndex(index);// 检查 index 范围

	if (index == size)// 如果 index==size，连接到当前链表的尾部
	linkLast(element);
	else
	linkBefore(element, node(index));
	}

	Node<E> node(int index) {
	// assert isElementIndex(index);
	/*
	index < (size>> 1) 采用二分思想，先将 index 与长度 size 的一半比较，如果 index<size/2，就只从位置 0
	往后遍历到位置 index 处，而如果 index>size/2，就只从位置 size 往前遍历到位置 index 处。这样可以减少一部
	分不必要的遍历。
	*/
	// 如果 index<size/2，就从前往后找目标结点
	if (index < (size >> 1)) {
	Node<E> x = first;
	for (int i = 0; i < index; i++)
	x = x.next;
	return x;
	} else {// 否则从后往前找目标结点
	Node<E> x = last;
	for (int i = size - 1; i > index; i--)
	x = x.prev;
	return x;
	}
	}

	// 把新结点插入到 [index] 位置的结点 succ 前面
	void linkBefore(E e, Node<E> succ) {//succ 是 [index] 位置对应的结点
	// assert succ != null;
	final Node<E> pred = succ.prev; //[index] 位置的前一个结点

	// 新结点的 prev 是原来 [index] 位置的前一个结点
	// 新结点的 next 是原来 [index] 位置的结点
	final Node<E> newNode = new Node<>(pred, e, succ);

	//[index] 位置对应的结点的 prev 指向新结点
	succ.prev = newNode;

	// 如果原来 [index] 位置对应的结点是第一个结点，那么现在新结点是第一个结点
	if (pred == null)
	first = newNode;
	else
	pred.next = newNode;// 原来 [index] 位置的前一个结点的 next 指向新结点
	size++;
	modCount++;
	}

	// 方法：remove () 相关方法
	public boolean remove(Object o) {
	// 分 o 是否为空两种情况
	if (o == null) {
	// 找到 o 对应的结点 x
	for (Node<E> x = first; x != null; x = x.next) {
	if (x.item == null) {
	unlink(x);// 删除 x 结点
	return true;
	}
	}
	} else {
	// 找到 o 对应的结点 x
	for (Node<E> x = first; x != null; x = x.next) {
	if (o.equals(x.item)) {
	unlink(x);// 删除 x 结点
	return true;
	}
	}
	}
	return false;
	}
	E unlink(Node<E> x) {//x 是要被删除的结点
	// assert x != null;
	final E element = x.item;// 被删除结点的数据
	final Node<E> next = x.next;// 被删除结点的下一个结点
	final Node<E> prev = x.prev;// 被删除结点的上一个结点

	// 如果被删除结点的前面没有结点，说明被删除结点是第一个结点
	if (prev == null) {
	// 那么被删除结点的下一个结点变为第一个结点
	first = next;
	} else {// 被删除结点不是第一个结点
	// 被删除结点的上一个结点的 next 指向被删除结点的下一个结点
	prev.next = next;
	// 断开被删除结点与上一个结点的链接
	x.prev = null;// 使得 GC 回收
	}

	// 如果被删除结点的后面没有结点，说明被删除结点是最后一个结点
	if (next == null) {
	// 那么被删除结点的上一个结点变为最后一个结点
	last = prev;
	} else {// 被删除结点不是最后一个结点
	// 被删除结点的下一个结点的 prev 执行被删除结点的上一个结点
	next.prev = prev;
	// 断开被删除结点与下一个结点的连接
	x.next = null;// 使得 GC 回收
	}
	// 把被删除结点的数据也置空，使得 GC 回收
	x.item = null;
	// 元素个数减少
	size--;
	// 修改次数增加
	modCount++;
	// 返回被删除结点的数据
	return element;
	}

	public E remove(int index) { //index 是要删除元素的索引位置
	checkElementIndex(index);
	return unlink(node(index));
	}

# 7.3.3 LinkedList 相关方法图示

只有 1 个元素的 LinkedList

包含 4 个元素的 LinkedList

add (E e) 方法

add (int index,E e) 方法

remove (Object obj) 方法

remove (int index) 方法

# 7.4 启示、开发建议

Vector 基本不用了
ArrayList 底层使用 数组
- 查找、尾部添加效率高， $O(1)$
- 插入、删除效率低， $O(n)$
LinkedList 底层使用 双向链表
- 查找效率低， $O(n)$
- 插入、删除效率高， $O(1)$
ArrayList 有两个构造器
- new ArrayList() ：创建长度为 10 的 Object [] 数组
- new ArrayList(int capacity) ：创建指定长度的数组
  开发中，如果能大体确认数组长度，推荐使用这种，因为 避免了扩容、复制数组带来的时空消耗

# 8. Map 接口分析

Map 接口的实现类	HashMap	LinkedHashMap	TreeMap	~~Hashtable~~	Properties
地位	主要实现类	HashMap 的子类		古老实现类	~~Hashtable~~ 的子类
底层实现	哈希表	哈希表 + 双向链表	红黑树	哈希表	哈希表
数据结构	一维数组 + 单向链表（+ 红黑树）	一维数组 + 单向链表（+ 红黑树） + 双向链表	红黑树	一维数组 + 单向链表	一维数组 + 单向链表
键、值是否允许为 null	是	是	键不能为 null，值可以为 null	键和值都不能为 null	键和值都不能为 null
是否线程安全	否	否	否	是，因此效率低	是，因此效率低
特点	查找、插入、删除速度快，但不保证元素的顺序	保证元素的插入 / 访问顺序	可以按照 key 中的指定属性的大小顺序进行遍历：①自然排序；②定制排序	线程安全，效率低	键和值都是 String 类型
性能	①查找、插入、删除速度快；②迭代遍历速度慢（因为和容量有关，需要遍历底层数组，以及每个数组元素对应的链表 / 红黑树，数组的长度就是 HashMap 的容量）	①插入、删除速度慢；②迭代遍历比 HashMap 快（因为只和实际数据有关，和容量无关）	查找、插入、删除速度慢（因为要维护红黑树的平衡、顺序）
内存	占用大，保存数组		占用小，保存节点
使用场景	快速的查找和插入，不要求元素的顺序	需要保持元素的插入顺序或者访问顺序	适用于需要有序的键值对集合	适用于需要线程安全的场景	以键值对的方式存储配置信息
补充说明	在 JDK8 引入红黑树	双向链表: 记录元素的添加顺序	①自然排序（key 所在类实现了 Comparable 接口）；②定制排序（在创建 TreeMap 时传入 Comparator 对象）；
要求 key	key 所在类要重写 `hashCode()` 和 `equals()`	与 HashMap 相同	key 必须是同一个类的对象	与 HashMap 相同	key 是 String 类
要求 value	value 所在类要重写 `equals()`	与 HashMap 相同	无	与 HashMap 相同	value 是 String 类
判断 key 相等的标准	hashCode 值相等；equals () 返回 true；	与 HashMap 相同	`containsKey()` ：当实现了 key 的排序后，需要两个 key 通过 compareTo () 方法或者 compare () 方法返回 0	与 HashMap 相同	String 中重写的 equals () 返回 true
判断 value 相等的标准	equals () 返回 true；	与 HashMap 相同		与 HashMap 相同	String 中重写的 equals () 返回 true

# 8.1 哈希表的物理结构

HashMap 和 Hashtable 底层都是 哈希表 （也称散列表），其中维护了一个长度为 2 的幂次方的 Node<K,V>[] table ，初始长度默认为 16 。

其中 Node<K,V> 是个 static内部类 ，实现了Map.Entry<K,V>接口，接口中声明了 getKey ()、getValue ()、setValue () 等方法。

数组的每一个索引位置被称为一个 桶(bucket) ，你添加的映射关系 (key,value) 最终都被封装为一个 Map.Entry 类型的对象，放到某个 table [index] 桶中。

使用数组的目的是查询和添加的效率高，可以根据索引直接定位到某个 table [index]。

# 8.2 HashMap 中数据添加过程

# 8.2.1 JDK7

# 1. HashMap 对象实例化过程

在底层创建了长度为 16 的 Entry<K,V>[] table 的数组

HashMap<String, Integer> hashMap = new HashMap<>();

源码 ：

	public HashMap() {
	// 构造一个具有默认初始容量（16）和默认负载因子（0.75f）的空 HashMap。
	this(DEFAULT_INITIAL_CAPACITY, DEFAULT_LOAD_FACTOR);
	}

	// 使用指定的初始容量和负载因子构造一个空的 HashMap。
	public HashMap(int initialCapacity, float loadFactor) {
	//...(特判：略)...

	// 寻找一个大于等于 initialCapacity 的 2 的幂次方 capacity
	int capacity = 1;
	while (capacity < initialCapacity)
	capacity <<= 1;

	this.loadFactor = loadFactor; // 确定加载因子
	threshold = (int)Math.min(capacity * loadFactor, MAXIMUM_CAPACITY + 1); // 确定阈值
	table = new Entry[capacity]; // 初始化数组，长度为 capacity，而不是传入的参数 initialCapacity

	//...（略）...
	}

其中的 成员变量 ：

	// 默认的初始化容量，必须是 2 的幂次方。
	static final int DEFAULT_INITIAL_CAPACITY = 16;
	// 最大容量，如果其中一个带有参数的构造函数隐式指定了更高的值，则使用该容量。必须是 2 的幂次方，且小于等于 1<<30。
	static final int MAXIMUM_CAPACITY = 1 << 30;
	// 默认的加载因子
	static final float DEFAULT_LOAD_FACTOR = 0.75f;

	// 存储 key-value 映射的数组，根据需要调整大小，长度必须是二的幂次方。
	transient Entry<K,V>[] table;
	// 实际存储的 key-value 映射的数量。
	transient int size;
	// 阈值（容量 * 加载因子）：当 size 达到该值时需要扩容
	int threshold;
	// 加载因子
	final float loadFactor;

# 2. put (key,value) 过程

put (key1,value1) 的过程：
调用 key1 所在类的 hashCode() 方法，计算 key1 的哈希值 1，经过某种算法（ hash() ）计算后得到哈希值 2
哈希值 2 再经过某种算法（ indexFor() ）后确定 (key1,value1) 在数组 table 中的存放位置 i（即为索引位置）
如果数组 table 的索引位置 i 上没有元素，则直接将 (key1,value1) 添加到该位置上 ————添加情况 1
如果数组 table 的索引位置 i 上有元素 (key2,value2)，则比较 key1 和 key2 的 哈希值2 ：————哈希冲突
如果二者的哈希值 2 不相同，则直接将 (key1,value1) 添加到该位置上 ————添加情况 2
如果二者的哈希值 2 相同，则继续比较 key1.equals(key2) ：
如果 false，说明二者不同，则直接将 (key1,value1) 添加到该位置上 ————添加情况 3
如果 true，说明二者相同，则用 value1 替换 value2，即修改数组 table 的索引位置 i 上的元素为 (key1,value1)，并返回原来的 value2————修改 value
哈希冲突：两个不同的 key 的哈希值相同
添加情况 1/2/3：将 (key1,value1) 以 ** 单向链表（头插法） ** 的方式链接到数组 table 的索引位置 i 上
随着不断添加元素，当满足 扩容条件(size >= threshold) && (null != table[i]) 时，会将数组 table 扩容为原来的 2 倍
其中 threshold = table 数组长度 * 加载因子 loadFactor（默认为 0.75 ），即初始阈值为 12
其中 (null != table [i])：表示数组 table 的索引位置 i 上有元素，即发生了哈希冲突，可能会导致链表过长，影响查找效率，所以需要扩容
加载因子 的意义:
过大会导致 table 数组用得久，内部元素过多，出现链表的概率增大， 查找效率降低 ，好处是 节省内存空间
过小会导致 table 数组的空间利用率低， 浪费内存空间 ，且 频繁扩容 费时

hashMap.put(key1,value1);

源码 ：

	public V put(K key, V value) {
	// 特判：HashMap 允许 key 为 null，此时将 (key1,value1) 存放到 table [0] 上
	if (key == null)
	return putForNullKey(value);

	int hash = hash(key);// 传入 key1，内部调用其 hashCode () 得到哈希值 1，并经过某种算法，返回哈希值 2
	int i = indexFor(hash, table.length);// 根据哈希值 2 确定 (key1,value1) 在数组 table 中的存放索引位置 i

	// 若 table [i] 为空，则不会进入 for 循环，对应添加情况 1。
	// 若 table [i] 上已有元素（key2,value2），即哈希冲突，则比较 key1 和 key2 的哈希值 2 是否相同。
	for (Entry<K,V> e = table[i]; e != null; e = e.next) {
	/**
	* 两种情况：
	* 1. for 循环遍历结束，没有进入过 if 代码块，
	* - 可能是 e.hash == hash 始终不满足，意味着 (key1,value1) 与 table [i] 对应 bucket 链表上的所有元素都不同，对应添加情况 2；
	* - 可能在遍历到链表上某个元素 e 时， e.hash == hash 满足，但是 key1.equals (e.key) 返回 false，还是不满足 if 条件，直到 for 循环结束，对应添加情况 3；
	* 2. for 循环遍历到某个元素 e 时进入了 if 代码块，即 e.hash 与 (key1,value1) 的 hash 相等，且 key1.equals (e.key)，此时用 value1 将 e.value 替换，对应修改 value 的情况。
	*/
	Object k;
	if (e.hash == hash && ((k = e.key) == key \|\| key.equals(k))) {
	V oldValue = e.value;// 记录旧 value
	e.value = value;// 更新 value
	e.recordAccess(this);
	return oldValue;// 修改成功：返回旧 value
	}
	}

	modCount++;
	addEntry(hash, key, value, i);// 添加情况 1/2/3（均为头插法）
	return null;// 添加成功：返回 null
	}

其中 putForNullKey() ：如果 key 是 null，单独处理，存储到 table [0] 中，如果有另一个 key 为 null，value 覆盖。

	private V putForNullKey(V value) {
	for (Entry<K,V> e = table[0]; e != null; e = e.next) {
	if (e.key == null) {
	V oldValue = e.value;
	e.value = value;
	e.recordAccess(this);
	return oldValue;
	}
	}
	modCount++;
	addEntry(0, null, value, 0);
	return null;
	}

其中 hash() ：检索哈希值 k，并将补充哈希函数应用于结果哈希，从而防止质量较差的哈希函数。这一点至关重要，因为 HashMap 使用的哈希表的长度是 2 的幂次方，否则会遇到低位不变的 hashCode 冲突。注意：null 键总是映射到哈希 0，从而映射到索引 0。

	final int hash(Object k) {
	int h = 0;
	if (useAltHashing) {
	if (k instanceof String) {
	return sun.misc.Hashing.stringHash32((String) k);
	}
	h = hashSeed;
	}

	h ^= k.hashCode();// 调用 key 的 hashCode ()，得到哈希值 1

	// This function ensures that hashCodes that differ only by
	// constant multiples at each bit position have a bounded
	// number of collisions (approximately 8 at default load factor).
	h ^= (h >>> 20) ^ (h >>> 12);
	return h ^ (h >>> 7) ^ (h >>> 4); // 经过某种算法，得到并返回哈希值 2
	}

其中 indexFor() ：根据哈希值 2 确定 (key,value) 在数组 table 中的存放索引位置 i

static int indexFor(int h, int length) {

     return h & (length-1); // 按位与运算，直接取哈希值 2 的若干低位，也解释了为什么限制数组长度 length 为 2 的幂次方，就是为了方便根据哈希值计算映射在数组中的存储位置 i。哈希值 2 中只有若干低位参与运算，不用所有位都参与！

其中 addEntry() ：将具有指定键 key、值 value 和哈希值 hash 的新条目添加到指定索引的 bucket 中。此方法的责任是在适当的情况下调整表的大小。子类重写它来改变 put 方法的行为。扩容条件：size 达到 threshold，且 table [i]!=null。

	void addEntry(int hash, K key, V value, int bucketIndex) {
	// 扩容条件
	if ((size >= threshold) && (null != table[bucketIndex])) {
	resize(2 * table.length); // 默认扩容为原来的 2 倍
	hash = (null != key) ? hash(key) : 0; // 重新计算 hash
	bucketIndex = indexFor(hash, table.length); // 重新计算存放位置的索引 i
	}

	createEntry(hash, key, value, bucketIndex);
	}

其中 createEntry() ：与 addEntry 类似，不同之处在于此版本是在作为 Map 构造或 “伪构造”（克隆、反序列化）的一部分创建条目时使用的。这个版本不必担心调整表的大小。子类覆盖此项以更改 HashMap（Map）、clone 和 readObject 的行为。

	void createEntry(int hash, K key, V value, int bucketIndex) {
	Entry<K,V> e = table[bucketIndex];// 暂存 table [i] 原有元素，可以是 null
	table[bucketIndex] = new Entry<>(hash, key, value, e);// 将新元素封装到 Entry 对象中，同时其 next 指向原有元素（头插法）
	size++;
	}

# 3. 内部类 Entry<K,V> 的定义

	static class Entry<K,V> implements Map.Entry<K,V>{
	// 成员变量
	final K key;
	V value;
	Entry<K,V> next; // 指向 table [i] 上的原有元素，空则为 null，这是头插法的体现！
	int hash; // 在存储时，将 key 计算得到的哈希值 2 保存下来

	// 构造器
	Entry(int h, K k, V v, Entry<K,V> n) {
	value = v;
	next = n;
	key = k;
	hash = h;
	}

	// 成员方法（略）
	}

# 其他

	map.get(key1);
	/*
	① 计算 key1 的 hash 值，用这个方法 hash (key1)

	② 找 index = table.length-1 & hash;

	③ 如果 table [index] 不为空，那么就挨个比较哪个 Entry 的 key 与它相同，就返回它的 value
	*/

	map.remove(key1);
	/*
	① 计算 key1 的 hash 值，用这个方法 hash (key1)

	② 找 index = table.length-1 & hash;

	③ 如果 table [index] 不为空，那么就挨个比较哪个 Entry 的 key 与它相同，就删除它，把它前面的 Entry 的 next 的值修改为被删除 Entry 的 next
	*/

# 8.2.2 JDK8

HashMap 在 JDK7 和 JDK8 之间的区别：

其中数组初始化的区别与 ArrayList 在 JDK7 和 JDK8 之间的区别类似。

HashMap 的变化	JDK7	JDK8
table 数组类型	Entry<K,V>[]	`Node<K,V>` []
创建 HashMap 实例时	默认初始化数组的容量是 16（饿汉式）	没有初始化 table 数组（当首次添加映射元素时才将数组的容量初始化为 16）（ `懒汉式` ）
映射元素的添加方式（七上八下）	数组 + 单向链表（ `头插法` ）	数组 + 单向链表（ `尾插法` ） + `红黑树`
单向链表←→红黑树	×	当某个索引位置 i 上的链表的长度达到 8，且数组的长度超过 64时，此索引位置上的元素要从单向链表改为红黑树，将增删改查的时间复杂度从 $O(n)$ 降到 $O(log n)$ 。如果索引 i 位置是红黑树的结构，当不断删除元素的情况下，当前索引 i 位置上的元素的个数低于 6 时，要从红黑树改为单向链表，节省内存空间。
扩容条件	size 达到 threshold，且 table [i]!=null	size 达到 threshold，且 table [i]!=null；链表的长度达到 8，但数组的长度未超过 64

# 8.3 HashMap 源码剖析

# 8.3.1 JDK1.7.0_07 中源码

# 1、Entry

key-value 被封装为 HashMap.Entry 类型，而这个类型实现了 Map.Entry 接口。

	public class HashMap<K,V>{
	transient Entry<K,V>[] table;

	static class Entry<K,V> implements Map.Entry<K,V> {
	final K key;
	V value;
	Entry<K,V> next;
	int hash;

	/**
	* Creates new entry.
	*/
	Entry(int h, K k, V v, Entry<K,V> n) {
	value = v;
	next = n;
	key = k;
	hash = h;
	}
	// 略
	}
	}

# 2、属性

	//table 数组的默认初始化长度
	static final int DEFAULT_INITIAL_CAPACITY = 16;
	// 哈希表
	transient Entry<K,V>[] table;
	// 哈希表中 key-value 的个数
	transient int size;
	// 临界值、阈值（扩容的临界值）
	int threshold;
	// 加载因子
	final float loadFactor;
	// 默认加载因子
	static final float DEFAULT_LOAD_FACTOR = 0.75f;

# 3、构造器

	public HashMap() {
	//DEFAULT_INITIAL_CAPACITY：默认初始容量 16
	//DEFAULT_LOAD_FACTOR：默认加载因子 0.75
	this(DEFAULT_INITIAL_CAPACITY, DEFAULT_LOAD_FACTOR);
	}

	public HashMap(int initialCapacity, float loadFactor) {
	// 校验 initialCapacity 合法性
	if (initialCapacity < 0)
	throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity);
	// 校验 initialCapacity 合法性
	if (initialCapacity > MAXIMUM_CAPACITY)
	initialCapacity = MAXIMUM_CAPACITY;
	// 校验 loadFactor 合法性
	if (loadFactor <= 0 \|\| Float.isNaN(loadFactor))
	throw new IllegalArgumentException("Illegal load factor: " + loadFactor);

	// 计算得到 table 数组的长度（保证 capacity 是 2 的整次幂）
	int capacity = 1;
	while (capacity < initialCapacity)
	capacity <<= 1;
	// 加载因子，初始化为 0.75
	this.loadFactor = loadFactor;
	//threshold 初始为默认容量
	threshold = (int)Math.min(capacity * loadFactor, MAXIMUM_CAPACITY + 1);
	// 初始化 table 数组
	table = new Entry[capacity];
	useAltHashing = sun.misc.VM.isBooted() &&
	(capacity >= Holder.ALTERNATIVE_HASHING_THRESHOLD);
	init();
	}

# 4、put () 方法

	public V put(K key, V value) {
	// 如果 key 是 null，单独处理，存储到 table [0] 中，如果有另一个 key 为 null，value 覆盖
	if (key == null)
	return putForNullKey(value);
	// 对 key 的 hashCode 进行干扰，算出一个 hash 值
	/*
	hashCode 值 xxxxxxxxxx
	table.length-1 000001111

	hashCode 值 xxxxxxxxxx 无符号右移几位和原来的 hashCode 值做 ^ 运算，使得 hashCode 高位二进制值参与计算，
	也发挥作用，降低 index 冲突的概率。
	*/
	int hash = hash(key);
	// 计算新的映射关系应该存到 table [i] 位置，
	//i = hash & table.length-1，可以保证 i 在 [0,table.length-1] 范围内
	int i = indexFor(hash, table.length);
	// 检查 table [i] 下面有没有 key 与我新的映射关系的 key 重复，如果重复替换 value
	for (Entry<K,V> e = table[i]; e != null; e = e.next) {
	Object k;
	if (e.hash == hash && ((k = e.key) == key \|\| key.equals(k))) {
	V oldValue = e.value;
	e.value = value;
	e.recordAccess(this);
	return oldValue;
	}
	}

	modCount++;
	// 添加新的映射关系
	addEntry(hash, key, value, i);
	return null;
	}

其中，

	// 如果 key 是 null，直接存入 [0] 的位置
	private V putForNullKey(V value) {
	// 判断是否有重复的 key，如果有重复的，就替换 value
	for (Entry<K,V> e = table[0]; e != null; e = e.next) {
	if (e.key == null) {
	V oldValue = e.value;
	e.value = value;
	e.recordAccess(this);
	return oldValue;
	}
	}
	modCount++;
	// 把新的映射关系存入 [0] 的位置，而且 key 的 hash 值用 0 表示
	addEntry(0, null, value, 0);
	return null;
	}

	final int hash(Object k) {
	int h = 0;
	if (useAltHashing) {
	if (k instanceof String) {
	return sun.misc.Hashing.stringHash32((String) k);
	}
	h = hashSeed;
	}

	h ^= k.hashCode();

	// This function ensures that hashCodes that differ only by
	// constant multiples at each bit position have a bounded
	// number of collisions (approximately 8 at default load factor).
	h ^= (h >>> 20) ^ (h >>> 12);
	return h ^ (h >>> 7) ^ (h >>> 4);
	}

	static int indexFor(int h, int length) {
	return h & (length-1);
	}

	void addEntry(int hash, K key, V value, int bucketIndex) {
	// 判断是否需要库容
	// 扩容：（1）size 达到阈值（2）table [i] 正好非空
	if ((size >= threshold) && (null != table[bucketIndex])) {
	//table 扩容为原来的 2 倍，并且扩容后，会重新调整所有 key-value 的存储位置
	resize(2 * table.length);
	// 新的 key-value 的 hash 和 index 也会重新计算
	hash = (null != key) ? hash(key) : 0;
	bucketIndex = indexFor(hash, table.length);
	}
	// 存入 table 中
	createEntry(hash, key, value, bucketIndex);
	}

	void createEntry(int hash, K key, V value, int bucketIndex) {
	Entry<K,V> e = table[bucketIndex];
	// 原来 table [i] 下面的映射关系作为新的映射关系 next
	table[bucketIndex] = new Entry<>(hash, key, value, e);
	// 个数增加
	size++;
	}

# 8.3.2 JDK1.8.0_271 中源码

# 1、Node

key-value 被封装为 HashMap.Node<K,V> 类型或 HashMap.TreeNode<K,V> 类型，它俩都直接或间接的实现了 Map.Entry 接口。

存储到 table 数组的可能是 Node 结点对象，也可能是 TreeNode 结点对象，它们也是 Map.Entry 接口的实现类。即 table [index] 下的映射关系可能串起来一个 单向链表 或一棵 红黑树 。

	public class HashMap<K,V>{
	transient Node<K,V>[] table;

	//Node 类
	static class Node<K,V> implements Map.Entry<K,V> {
	final int hash;
	final K key;
	V value;
	Node<K,V> next;

	Node(int hash, K key, V value, Node<K,V> next) {
	this.hash = hash;
	this.key = key;
	this.value = value;
	this.next = next;
	}
	// 其它结构：略
	}

	//TreeNode 类
	static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
	TreeNode<K,V> parent;
	TreeNode<K,V> left;
	TreeNode<K,V> right;
	TreeNode<K,V> prev;
	boolean red; // 是红结点还是黑结点
	TreeNode(int hash, K key, V val, Node<K,V> next) {
	super(hash, key, val, next);
	}
	}

	//....
	}

# 2、属性

当单个的链表的结点个数达到 8，并且 table 的长度达到 64，才会 树化 。
当单个的链表的结点个数达到 8，但是 table 的长度未达到 64，会先 扩容 。

	static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // 默认的初始容量 16
	static final int MAXIMUM_CAPACITY = 1 << 30; // 最大容量 1 << 30
	static final float DEFAULT_LOAD_FACTOR = 0.75f; // 默认加载因子
	static final int TREEIFY_THRESHOLD = 8; // 默认树化阈值 8，当链表的长度达到这个值后，要考虑树化
	static final int UNTREEIFY_THRESHOLD = 6;// 默认反树化阈值 6，当树中结点的个数达到此阈值后，要考虑变为链表

	static final int MIN_TREEIFY_CAPACITY = 64; // 最小树化容量 64

	transient Node<K,V>[] table; // 数组
	transient int size; // 记录有效映射关系的对数，也是 Entry 对象的个数
	int threshold; // 阈值，当 size 达到阈值时，考虑扩容
	final float loadFactor; // 加载因子，影响扩容的频率

# 3、构造器

	public HashMap() {
	this.loadFactor = DEFAULT_LOAD_FACTOR; //all other fields defaulted (其他字段都是默认值)
	}

# 4、put () 方法

public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}

其中，

	static final int hash(Object key) {
	int h;
	// 如果 key 是 null，hash 是 0
	// 如果 key 非 null，用 key 的 hashCode 值与 key 的 hashCode 值高 16 进行异或
	// 即就是用 key 的 hashCode 值高 16 位与低 16 位进行了异或的干扰运算

	/*
	index = hash & table.length-1
	如果用 key 的原始的 hashCode 值与 table.length-1 进行按位与，那么基本上高 16 没机会用上。
	这样就会增加冲突的概率，为了降低冲突的概率，把高 16 位加入到 hash 信息中。
	*/
	return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
	}

	final V putVal(int hash, K key, V value, boolean onlyIfAbsent,boolean evict) {
	Node<K,V>[] tab; // 数组
	Node<K,V> p; // 一个结点
	int n, i; //n 是数组的长度 i 是下标

	//tab 和 table 等价
	// 如果 table 是空的
	if ((tab = table) == null \|\| (n = tab.length) == 0){
	n = (tab = resize()).length;
	/*
	tab = resize();
	n = tab.length;*/
	/*
	如果 table 是空的，resize () 完成了①创建了一个长度为 16 的数组②threshold = 12
	n = 16
	*/
	}
	//i = (n - 1) & hash ，下标 = 数组长度 - 1 & hash
	//p = tab [i] 第 1 个结点
	//if (p==null) 条件满足的话说明 table [i] 还没有元素
	if ((p = tab[i = (n - 1) & hash]) == null){
	// 把新的映射关系直接放入 table [i]
	tab[i] = newNode(hash, key, value, null);
	//newNode（）方法就创建了一个 Node 类型的新结点，新结点的 next 是 null
	}else {
	Node<K,V> e; K k;
	//p 是 table [i] 中第一个结点
	//if (table [i] 的第一个结点与新的映射关系的 key 重复)
	if (p.hash == hash &&
	((k = p.key) == key \|\| (key != null && key.equals(k))))
	e = p;// 用 e 记录这个 table [i] 的第一个结点
	else if (p instanceof TreeNode){ // 如果 table [i] 第一个结点是一个树结点
	// 单独处理树结点
	// 如果树结点中，有 key 重复的，就返回那个重复的结点用 e 接收，即 e!=null
	// 如果树结点中，没有 key 重复的，就把新结点放到树中，并且返回 null，即 e=null
	e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
	}else {
	//table [i] 的第一个结点不是树结点，也与新的映射关系的 key 不重复
	//binCount 记录了 table [i] 下面的结点的个数
	for (int binCount = 0; ; ++binCount) {
	// 如果 p 的下一个结点是空的，说明当前的 p 是最后一个结点
	if ((e = p.next) == null) {
	// 把新的结点连接到 table [i] 的最后
	p.next = newNode(hash, key, value, null);
	// 如果 binCount>=8-1，达到 7 个时
	if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
	// 要么扩容，要么树化
	treeifyBin(tab, hash);
	break;
	}
	// 如果 key 重复了，就跳出 for 循环，此时 e 结点记录的就是那个 key 重复的结点
	if (e.hash == hash &&
	((k = e.key) == key \|\| (key != null && key.equals(k))))
	break;
	p = e;// 下一次循环，e=p.next，就类似于 e=e.next，往链表下移动
	}
	}
	// 如果这个 e 不是 null，说明有 key 重复，就考虑替换原来的 value
	if (e != null) { // existing mapping for key
	V oldValue = e.value;
	if (!onlyIfAbsent \|\| oldValue == null)
	e.value = value;
	afterNodeAccess(e); // 什么也没干
	return oldValue;
	}
	}
	++modCount;

	// 元素个数增加
	//size 达到阈值
	if (++size > threshold)
	resize(); // 一旦扩容，重新调整所有映射关系的位置
	afterNodeInsertion(evict); // 什么也没干
	return null;
	}

	final Node<K,V>[] resize() {
	Node<K,V>[] oldTab = table; //oldTab 原来的 table
	//oldCap：原来数组的长度
	int oldCap = (oldTab == null) ? 0 : oldTab.length;
	//oldThr：原来的阈值
	int oldThr = threshold;// 最开始 threshold 是 0

	//newCap，新容量
	//newThr：新阈值
	int newCap, newThr = 0;
	if (oldCap > 0) { // 说明原来不是空数组
	if (oldCap >= MAXIMUM_CAPACITY) { // 是否达到数组最大限制
	threshold = Integer.MAX_VALUE;
	return oldTab;
	}
	else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
	oldCap >= DEFAULT_INITIAL_CAPACITY)
	//newCap = 旧的容量 * 2 ，新容量 & lt; 最大数组容量限制
	// 新容量：32,64，...
	//oldCap >= 初始容量 16
	// 新阈值重新算 = 24，48 ....
	newThr = oldThr << 1; // double threshold
	}
	else if (oldThr > 0) // initial capacity was placed in threshold
	newCap = oldThr;
	else { // zero initial threshold signifies using defaults
	newCap = DEFAULT_INITIAL_CAPACITY; // 新容量是默认初始化容量 16
	// 新阈值 = 默认的加载因子 * 默认的初始化容量 = 0.75*16 = 12
	newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
	}
	if (newThr == 0) {
	float ft = (float)newCap * loadFactor;
	newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
	(int)ft : Integer.MAX_VALUE);
	}
	threshold = newThr; // 阈值赋值为新阈值 12，24.。。。
	// 创建了一个新数组，长度为 newCap，16，32,64.。。
	@SuppressWarnings({"rawtypes","unchecked"})
	Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
	table = newTab;
	if (oldTab != null) { // 原来不是空数组
	// 把原来的 table 中映射关系，倒腾到新的 table 中
	for (int j = 0; j < oldCap; ++j) {
	Node<K,V> e;
	if ((e = oldTab[j]) != null) {//e 是 table 下面的结点
	oldTab[j] = null; // 把旧的 table [j] 位置清空
	if (e.next == null) // 如果是最后一个结点
	newTab[e.hash & (newCap - 1)] = e; // 重新计算 e 的在新 table 中的存储位置，然后放入
	else if (e instanceof TreeNode) // 如果 e 是树结点
	// 把原来的树拆解，放到新的 table
	((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
	else { // preserve order
	Node<K,V> loHead = null, loTail = null;
	Node<K,V> hiHead = null, hiTail = null;
	Node<K,V> next;
	// 把原来 table [i] 下面的整个链表，重新挪到了新的 table 中
	do {
	next = e.next;
	if ((e.hash & oldCap) == 0) {
	if (loTail == null)
	loHead = e;
	else
	loTail.next = e;
	loTail = e;
	}
	else {
	if (hiTail == null)
	hiHead = e;
	else
	hiTail.next = e;
	hiTail = e;
	}
	} while ((e = next) != null);
	if (loTail != null) {
	loTail.next = null;
	newTab[j] = loHead;
	}
	if (hiTail != null) {
	hiTail.next = null;
	newTab[j + oldCap] = hiHead;
	}
	}
	}
	}
	}
	return newTab;
	}

	Node<K,V> newNode(int hash, K key, V value, Node<K,V> next) {
	// 创建一个新结点
	return new Node<>(hash, key, value, next);
	}

	final void treeifyBin(Node<K,V>[] tab, int hash) {
	int n, index;
	Node<K,V> e;
	//MIN_TREEIFY_CAPACITY：最小树化容量 64
	// 如果 table 是空的，或者 table 的长度没有达到 64
	if (tab == null \|\| (n = tab.length) < MIN_TREEIFY_CAPACITY)
	resize();// 先扩容
	else if ((e = tab[index = (n - 1) & hash]) != null) {
	// 用 e 记录 table [index] 的结点的地址
	TreeNode<K,V> hd = null, tl = null;
	/*
	do...while，把 table [index] 链表的 Node 结点变为 TreeNode 类型的结点
	*/
	do {
	TreeNode<K,V> p = replacementTreeNode(e, null);
	if (tl == null)
	hd = p;//hd 记录根结点
	else {
	p.prev = tl;
	tl.next = p;
	}
	tl = p;
	} while ((e = e.next) != null);

	// 如果 table [index] 下面不是空
	if ((tab[index] = hd) != null)
	hd.treeify(tab);// 将 table [index] 下面的链表进行树化
	}
	}

# 小结

# 8.4 LinkedHashMap 源码剖析

LinkedHashMap 是 HashMap 的子类。在 “数组 + 单向链表 + 红黑树” 的基础上，增加了一对 双向链表 ，记录映射元素的添加顺序，便于遍历。

# 8.4.1 图示

# 8.4.2 源码

内部类 Entry<K,V> 继承自 HashMap.Node<K,V> 如下：

添加了两个属性 before 和 after ，分别指向添加顺序上的前、后元素。
注意区分 after与next ：后者指向的是链表上的下一个元素，不一定是添加顺序上的下一个元素。

	static class Entry<K,V> extends HashMap.Node<K,V> {
	Entry<K,V> before, after;

	Entry(int hash, K key, V value, Node<K,V> next) {
	super(hash, key, value, next);
	}
	}

LinkedHashMap 重写了 HashMap 中的 newNode() 方法：

因为要考虑 双向链表 在添加元素中的表现，即 before、after 如何指向。

	Node<K,V> newNode(int hash, K key, V value, Node<K,V> e) {
	LinkedHashMap.Entry<K,V> p =
	new LinkedHashMap.Entry<K,V>(hash, key, value, e);
	linkNodeLast(p);
	return p;
	}

	TreeNode<K,V> newTreeNode(int hash, K key, V value, Node<K,V> next) {
	TreeNode<K,V> p = new TreeNode<K,V>(hash, key, value, next);
	linkNodeLast(p);
	return p;
	}

# 9. Set 接口分析

# 9.1 Set 集合与 Map 集合的关系

Set 的内部实现其实是一个 Map，Set 中的元素，存储在 Map 的 key 中，而 Map 的 value 置为一个 Object 常量。

HashSet 的内部实现是一个 HashMap
TreeSet 的内部实现是一个 TreeMap
LinkedHashSet 的内部实现是一个 LinkedHashMap

# 9.2 源码剖析

HashSet 源码：

	// 构造器
	public HashSet() {
	map = new HashMap<>();
	}

	public HashSet(int initialCapacity, float loadFactor) {
	map = new HashMap<>(initialCapacity, loadFactor);
	}

	public HashSet(int initialCapacity) {
	map = new HashMap<>(initialCapacity);
	}

	// 这个构造器是给子类 LinkedHashSet 调用的
	HashSet(int initialCapacity, float loadFactor, boolean dummy) {
	map = new LinkedHashMap<>(initialCapacity, loadFactor);
	}

	//add () 方法：
	public boolean add(E e) {
	return map.put(e, PRESENT)==null;
	}
	// 其中，
	private transient HashMap<E,Object> map;
	private static final Object PRESENT = new Object();

	//iterator () 方法：
	public Iterator<E> iterator() {
	return map.keySet().iterator();
	}

LinkedHashSet 源码：

	// 构造器
	public LinkedHashSet() {
	super(16, .75f, true);
	}
	public LinkedHashSet(int initialCapacity) {
	super(initialCapacity, .75f, true);// 调用 HashSet 的某个构造器
	}
	public LinkedHashSet(int initialCapacity, float loadFactor) {
	super(initialCapacity, loadFactor, true);// 调用 HashSet 的某个构造器
	}

TreeSet 源码：

	public TreeSet() {
	this(new TreeMap<E,Object>());
	}

	TreeSet(NavigableMap<E,Object> m) {
	this.m = m;
	}
	// 其中，
	private transient NavigableMap<E,Object> m;

	//add () 方法：
	public boolean add(E e) {
	return m.put(e, PRESENT)==null;
	}
	// 其中，
	private static final Object PRESENT = new Object();

# 10. 【拓展】HashMap 的相关问题

# 1、说说你理解的哈希算法

hash 算法是一种可以从任何数据中提取出其 “指纹” 的 数据摘要算法 ，它将任意大小的数据映射到一个固定大小的序列上，这个序列被称为hash code、数据摘要或者指纹。比较出名的 hash 算法有 MD5、SHA。hash 是具有 唯一性 且 不可逆 的，唯一性是指相同的 “对象” 产生的 hash code 永远是一样的。

1563797150134

# 2、Entry 中的 hash 属性为什么不直接使用 key 的 hashCode () 返回值呢？

省流：问你hash () 的作用

不管是 JDK1.7 还是 JDK1.8 中，都不是直接用 key 的 hashCode 值直接与 table.length-1 计算求下标的，而是先对 key 的 hashCode 值进行了一个运算，JDK1.7 和 JDK1.8 关于 hash () 的实现代码不一样，但是不管怎么样都是为了提高 hash code 值与 (table.length-1) 的按位与完的结果，尽量的均匀分布。

JDK1.7：

	final int hash(Object k) {
	int h = hashSeed;
	if (0 != h && k instanceof String) {
	return sun.misc.Hashing.stringHash32((String) k);
	}

	h ^= k.hashCode();
	h ^= (h >>> 20) ^ (h >>> 12);
	return h ^ (h >>> 7) ^ (h >>> 4);
	}

JDK1.8：

	static final int hash(Object key) {
	int h;
	return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
	}

虽然算法不同，但是思路都是将 hashCode 值的高位二进制与低位二进制值进行了异或，让高位二进制参与到 index 的计算中，增强随机性。

为什么要 hashCode 值的二进制的高位参与到 index 计算呢？

因为一个 HashMap 的 table 数组一般不会特别大，至少在不断扩容之前，那么 table.length-1 的大部分高位都是 0，直接用 hashCode 和 table.length-1 进行 & 运算的话，就会导致总是只有最低的几位是有效的，那么就算你的 hashCode () 实现的再好也难以避免发生碰撞，这时让高位参与进来的意义就体现出来了。高位参与的意义：对 hashcode 的低位添加了随机性，并且混合了高位的部分特征，显著减少了碰撞冲突的发生。

# 3、HashMap 是如何决定某个 key-value 存在哪个桶（bucket）的呢？

因为 hash 值是一个整数，而数组的长度也是一个整数，有两种思路：

hash 值 % table.length 会得到一个 [0,table.length-1] 范围的值，正好是下标范围，但是用% 运算效率没有位运算符 & 高。
hash 值 & (table.length-1) ，任何数 & (table.length-1) 的结果也一定在 [0, table.length-1] 范围。

1563800372286

JDK1.7：

	static int indexFor(int h, int length) {
	// assert Integer.bitCount(length) == 1 : "length must be a non-zero power of 2";
	return h & (length-1); // 此处 h 就是 hash
	}

JDK1.8：

	final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
	Node<K,V>[] tab; Node<K,V> p; int n, i;
	if ((tab = table) == null \|\| (n = tab.length) == 0)
	n = (tab = resize()).length;
	if ((p = tab[i = (n - 1) & hash]) == null) // i = (n - 1) & hash
	tab[i] = newNode(hash, key, value, null);
	//.... 省略大量代码
	}

# 4、为什么要保持 table 数组一直是 2 的 n 次幂呢？

因为如果数组的长度为 2 的 n 次幂，那么 table.length-1的二进制就是一个高位全是0，低位全是1的数字 ，这样才能保证在计算 index = hash 值 & (table.length-1) 时，index 的取值在 [0,table.length-1] 范围上，即数组的每一个下标位置都有机会被用到。

举例 1：

	hashCode值是？
	table.length是10
	table.length-1是9

	？ ????????
	9 00001001
	&_____________
	00000000 [0]
	00000001 [1]
	00001000 [8]
	00001001 [9]
	一定[0]~[9]

举例 2：

	hashCode值是？
	table.length是16
	table.length-1是15

	？ ????????
	15 00001111
	&_____________
	00000000 [0]
	00000001 [1]
	00000010 [2]
	00000011 [3]
	...
	00001111 [15]
	范围是[0,15]，一定在[0,table.length-1]范围内

# 5、解决 [index] 冲突问题

虽然从设计 hashCode () 到上面 HashMap 的 hash () 函数，都尽量减少冲突，但是仍然存在两个不同的对象返回的 hashCode 值相同，或者 hashCode 值就算不同，通过 hash () 函数计算后，得到的 index 也会存在大量的相同，因此 key 分布完全均匀的情况是不存在的。那么发生 碰撞冲突 时怎么办？

JDK1.8 之前使用：数组 + 单向链表的结构。

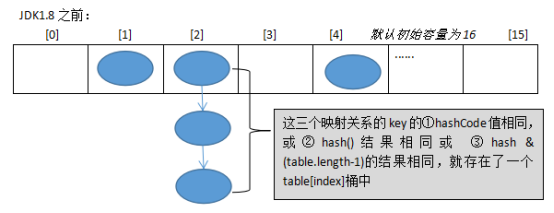
1563802656661

JDK1.8 之后使用：数组 + 链表 / 红黑树的结构。

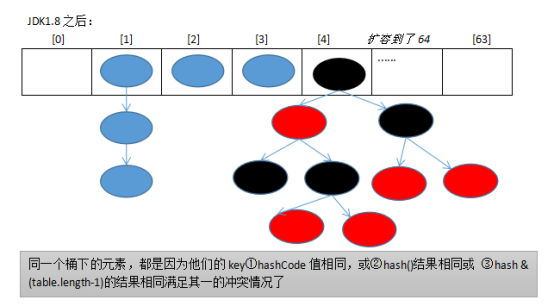
1563802665708

即 hash 相同或 hash&(table.lengt-1) 的值相同，那么就存入同一个 “桶” table [index] 中，使用 单向链表 或 红黑树 连接起来。

# 6、为什么 JDK1.8 会出现红黑树和链表共存呢？

因为当冲突比较严重时，table [index] 下面的链表就会很长，那么会导致查找效率降低，而如果此时将链表转化为二叉树，可以大大提高增、删、改、查的效率。

但是二叉树的结构又过于复杂，占用内存也较多，如果结点个数比较少的时候，那么选择链表反而更简单。

所以会出现红黑树和链表共存。

# 7、加载因子的值大小有什么关系？

如果太大，threshold 就会很大，那么如果冲突比较严重的话，就会导致 table [index] 下面的结点个数很多，影响效率。

如果太小，threshold 就会很小，那么数组扩容的频率就会提高，数组的使用率也会降低，那么会造成空间的浪费。

# 8、什么时候树化？什么时候反树化？

	static final int TREEIFY_THRESHOLD = 8;// 树化阈值
	static final int UNTREEIFY_THRESHOLD = 6;// 反树化阈值
	static final int MIN_TREEIFY_CAPACITY = 64;// 最小树化容量

链表 -> 红黑树：当某 table [index] 下的 链表的结点个数达到8 ，并且 table.length>=64 ，那么如果新 Entry 对象还添加到该 table [index] 中，那么就会将 table [index] 的链表进行树化。
红黑树 -> 链表：当某 table [index] 下的 红黑树结点个数少于6个 ，此时，
- 当继续删除 table [index] 下的树结点，最后这个根结点的左右结点有 null，或根结点的左结点的左结点为 null，会反树化
- 当重新添加新的映射关系到 map 中，导致了 map 重新扩容了，这个时候如果 table [index] 下面还是小于等于 6 的个数，那么会反树化

	package com.atguigu.map;

	public class MyKey{
	int num;

	public MyKey(int num) {
	super();
	this.num = num;
	}

	@Override
	public int hashCode() {
	if(num<=20){
	return 1;
	}else{
	final int prime = 31;
	int result = 1;
	result = prime * result + num;
	return result;
	}
	}

	@Override
	public boolean equals(Object obj) {
	if (this == obj)
	return true;
	if (obj == null)
	return false;
	if (getClass() != obj.getClass())
	return false;
	MyKey other = (MyKey) obj;
	if (num != other.num)
	return false;
	return true;
	}

	}

	package com.atguigu.map;

	import org.junit.Test;

	import java.util.HashMap;

	public class TestHashMapMyKey {
	@Test
	public void test1(){
	// 这里为了演示的效果，我们造一个特殊的类，这个类的 hashCode（）方法返回固定值 1
	// 因为这样就可以造成冲突问题，使得它们都存到 table [1] 中
	HashMap<MyKey, String> map = new HashMap<>();
	for (int i = 1; i <= 11; i++) {
	map.put(new MyKey(i), "value"+i);// 树化演示
	}
	}
	@Test
	public void test2(){
	HashMap<MyKey, String> map = new HashMap<>();
	for (int i = 1; i <= 11; i++) {
	map.put(new MyKey(i), "value"+i);
	}
	for (int i = 1; i <=11; i++) {
	map.remove(new MyKey(i));// 反树化演示
	}
	}
	@Test
	public void test3(){
	HashMap<MyKey, String> map = new HashMap<>();
	for (int i = 1; i <= 11; i++) {
	map.put(new MyKey(i), "value"+i);
	}

	for (int i = 1; i <=5; i++) {
	map.remove(new MyKey(i));
	}//table [1] 下剩余 6 个结点

	for (int i = 21; i <= 100; i++) {
	map.put(new MyKey(i), "value"+i);// 添加到扩容时，反树化
	}
	}
	}

# 9、key-value 中的 key 是否可以修改？

key-value 存储到 HashMap 中会存储 key 的 hash 值，这样就不用在每次查找时重新计算每一个 Entry 或 Node（TreeNode）的 hash 值了，因此如果已经 put 到 Map 中的 key-value，再修改 key 的属性，而这个属性又参与 hashcode 值的计算，那么会导致匹配不上。

这个规则也同样适用于其他所有散列存储结构的集合（LinkedHashMap、HashSet、LinkedHashSet、Hashtable 等）。

# 10、JDK1.7 中 HashMap 的循环链表是怎么回事？如何解决？

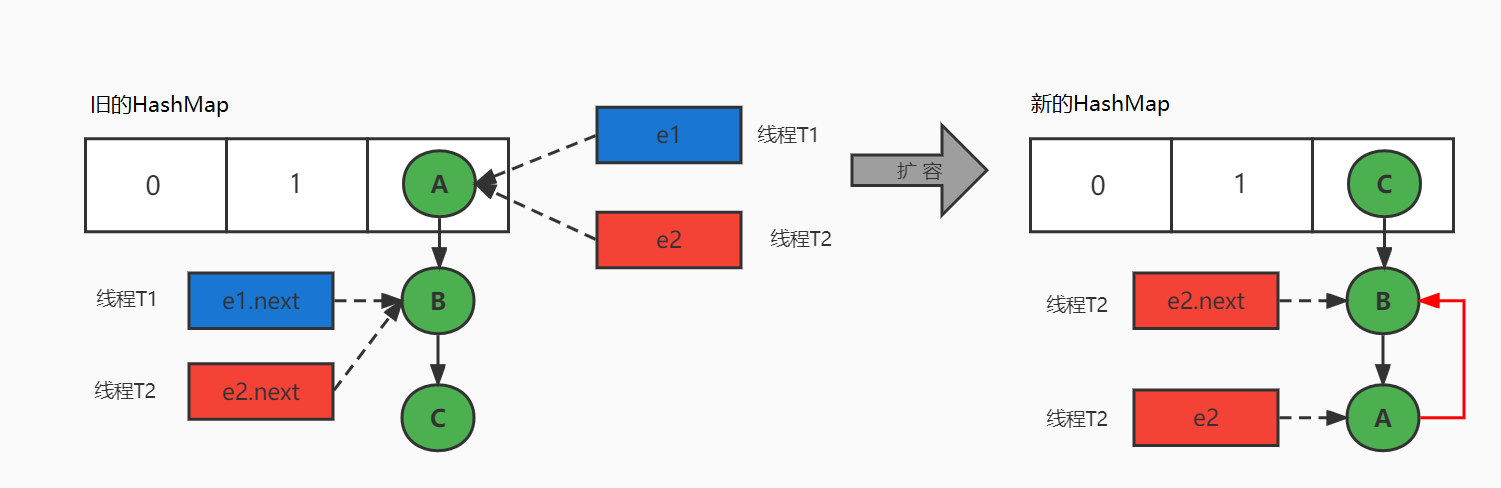
HashMap的循环引用问题

多线程环境下会出现该问题，避免 HashMap 发生死循环的常用解决方案：

多线程环境下，使用线程安全的 ConcurrentHashMap 替代 HashMap，推荐
多线程环境下，使用 synchronized 或 Lock 加锁，但会影响性能，不推荐
多线程环境下，使用线程安全的 Hashtable 替代，性能低，不推荐

HashMap 死循环只会发生在 JDK1.7 版本中，主要原因：头插法 + 链表 + 多线程并发 + 扩容。

在 JDK1.8 中，HashMap 改用 尾插法 ，解决了链表死循环的问题。

# 第 14 章_数据结构与集合源码

# 本章专题与脉络

# 1. 数据结构剖析

# 1.1 研究对象一：数据的逻辑结构

# 1.2 研究对象二：数据的存储结构（或物理结构）

# 1.3 研究对象三：运算结构

# 1.4 小结

# 2. 一维数组

# 2.1 数组的特点

# 2.2 自定义数组

# 3. 链表

# 3.1 链表的特点

# 3.2 自定义链表

# 3.2.1 自定义单向链表

# 3.2.2 自定义双向链表

# 4. 栈

# 4.1 栈的特点

# 4.2 Stack 使用举例

# 4.3 自定义栈

# 5. 队列

# 6. 树与二叉树

# 6.1 树的理解

# 6.2 二叉树的基本概念

# 6.3 二叉树的遍历

# 6.4 经典二叉树

# 6.5 二叉树及其结点的表示

# 7. List 接口分析

# 7.1 List 接口特点

# 7.2 动态数组 ArrayList 与 Vector

# 7.2.1 ArrayList 与 Vector 的区别

# 7.2.2 ArrayList 部分源码分析

# JDK1.7.0_07

# jdk1.8.0_271

# 7.2.3 ArrayList 相关方法图示

# 7.2.4 Vector 部分源码分析

# 7.3 链表 LinkedList

# 7.3.1 链表与动态数组的区别

# 7.3.2 LinkedList 源码分析

# 7.3.3 LinkedList 相关方法图示

# 7.4 启示、开发建议

# 8. Map 接口分析

# 8.1 哈希表的物理结构

# 8.2 HashMap 中数据添加过程

# 8.2.1 JDK7

# 1. HashMap 对象实例化过程

# 2. put (key,value) 过程

# 3. 内部类 Entry<K,V> 的定义

# 其他

# 8.2.2 JDK8

# 8.3 HashMap 源码剖析

# 8.3.1 JDK1.7.0_07 中源码

# 1、Entry

# 2、属性

# 3、构造器

# 4、put () 方法

# 8.3.2 JDK1.8.0_271 中源码

# 1、Node

# 2、属性

# 3、构造器

# 4、put () 方法

# 小结

# 8.4 LinkedHashMap 源码剖析

# 8.4.1 图示

# 8.4.2 源码

# 9. Set 接口分析

# 9.1 Set 集合与 Map 集合的关系

# 9.2 源码剖析

# 10. 【拓展】HashMap 的相关问题

# 1、说说你理解的哈希算法

# 2、Entry 中的 hash 属性为什么不直接使用 key 的 hashCode () 返回值呢？

# 3、HashMap 是如何决定某个 key-value 存在哪个桶（bucket）的呢？

# 4、为什么要保持 table 数组一直是 2 的 n 次幂呢？

# 5、解决 [index] 冲突问题

# 6、为什么 JDK1.8 会出现红黑树和链表共存呢？

# 7、加载因子的值大小有什么关系？

# 8、什么时候树化？什么时候反树化？

# 9、key-value 中的 key 是否可以修改？

# 10、JDK1.7 中 HashMap 的循环链表是怎么回事？如何解决？

宋红康_第13章_泛型(Generic)

宋红康_第15章_File类与IO流